太极 是由MIT的中国小伙胡渊鸣开发的一门编程语言。这不仅仅是又一个新的编程语言，我实在已经厌倦了不断有人造新的语言，来满足每个作者不同的语言怪癖。有许多的编程语言是没有存在的价值的，他们继续存在往往只是因为遗留历史项目还在维护。而『太极』是有开创性和工程价值的。

我认为太极有以下几个关键的有价值的特性：

1. 跨平台的GPU加速支持。同时支持CUDA、OpenGL、Metal，在Windows、Linux、MacOSX上都能很好的运行。我此前发现大部分的深度学习框架的GPU加速都是基于CUDA，这意味着我的macbook的GPU无法发挥作用。
2. 性能卓越，比PyTorch快13.4倍、Tensorflow要快188倍[1]。这两点都有着实实在在的经济价值。
3. 简洁易学。作者并没有想要特地标新立异，而是基于python的语法来开发，与python完全兼容。这是非常务实的，但并非没有追求的，代码是会被静态编译执行的，性能与C++代码并没有太多差别。

我认为太极在以下领域会有很好的应用：

1. 学术研究。
2. 机器学习、图形学、物理引擎、游戏编程的教学和实验。
3. 工具开发。可能作为最终产品的打包发布仍要探索，但制作工具是效率极高的。
4. 深度学习、离线渲染等离线任务的工程级应用。

对于一名仍在不断学习的中老年人而言，我不希望仅仅是学会一两个重复的工具，而是能够更高效的去实践、探索未知的世界。与其学习tensorflow这种集成式的深度学习框架，不如用太极自己实现一个，这样我们才能更深刻的理解其中的过程。我们还可以用太极将数据可视化的展示出来。

学习API是非常无趣的，但对于每一个学习编程的孩子来说，却是一道很高的门槛。很多人都无法实现在屏幕上绘制一个像素，这使我们哪怕拥有了足够的知识，依然缺乏表现力。有了太极，就仿佛打开了一道科研的大门。在科研过程中，我们需要的是快速实验、快速试错。太极就是为此而生的。

最近学习了一些计算机图形学的知识，重新点燃了自己想要学习游戏开发的热情。但是，计算机图形学与游戏开发还是有很大区别的。计算机图形学关心的是如何高质量的还原真实世界的视觉效果，而游戏开发则要求一个可编程性更强的系统。因此游戏引擎，首先是为开发服务的。

游戏引擎，应该允许游戏开发者，轻松的定义实体，操控这些实体的位置、模型、滤镜，最终通过渲染引擎渲染到屏幕上。甚至要提供一些易用的图形化制作工具，比如关卡编辑器，地图编辑器，实体编辑器，脚本语言，配置表，这些输出成数据文件。这些数据将被加载到内存，通过渲染引擎输出到屏幕。

[制作工具]–>静态数据–>[用户输入处理、AI update、物理引擎]–>动态数据–>[渲染引擎]–>最终画面。

游戏引擎=制作工具+程序API+渲染引擎。

而游戏引擎的关键，就在于处理数据。

哪怕一个最简单的终端贪食蛇游戏(这是我11岁的儿子写的)也需要符合这个标准。这个终端游戏制作工具不需要，他的素材是一些终端字符，google担任了这个制作工具的角色。程序API更新贪食蛇的动态数据，然后渲染引擎将动态数据映射成特定的终端字符打印在屏幕上。

开发一个3D游戏，数据结构更加复杂一些。理清了这个结构之后，3D游戏可能比2D游戏更容易开发一些，因为3D数据结构毕竟更接近真实世界。我们将整个待渲染的世界，称为【场景】，场景中摆放着各种【模型】。对于物理引擎部分，只需要模型的数据就可以了，而对于渲染引擎，则还需要【光源】和【摄像机】。

物理引擎

一个粒子由*位置position、速度velocity、质量mass、力force（加速度acceleration）、阻尼damping（简化一个物体在一个环境中的摩擦力如0.999）等属性，还需要考虑地心引力gravity的影响。

用反质量invertMass模拟无限质量？

位置更新公式：$$ p’=p+dot p t + 1/2 ddot p t^2 $$ 其中，$dot p$表示速度，$ddot p$表示加速度。在30fps时，t=0.033 后一项可以忽略。简化为 $$ p’=p+dot p t$$

速度更新公式: $$ dot p’ = dot p d^t + ddot p t $$ d为阻尼，

以上模拟对于慢速物体没有问题，但对于子弹、炮弹这种高速物体则不适用，因为可能在一帧之内子弹已穿过物体，无法与目标发生碰撞。因此对于这种情况，我们则需要将子弹想象为一个激光（或抛物线）。对于目标所受到的冲击，则需要通过动量守恒、能量守恒公式进行计算（TODO）。

重力是恒定的，但还有很多其他的力是动态生成的，爆炸、发射、风。因此我们要创造一个『力生成器』在每一帧执行它的updateForce方法，来设定物体受到的外力。

弹簧是一种普遍的模型，那些柔软的材质都可以抽象为大量的弹簧。根据胡克定理$$f=-k Delta l$$，我们可以写一个弹簧力生成器。

除了弹簧系统外，还有一类硬约束是紧密连接的对象，比如铁链、四肢。他们的关键在于连接点的速度是一致的。

然后我们要将所有的东西整合到一起成为一个物理引擎，在每一帧updatePhysics()

我们要将物理引擎从点升级到体，刚体的碰撞盒与他的质点。刚体的旋转。

碰撞检测（TODO）

参考：

《Game Physics Engine Development》2nd Edition by Ian Millington

双向反射分布函数（bidirectional reflectance distribution function）$f_r(omega_i,omega_r)$是一个计算光照反射量的函数。$omega_i$表示输入光角度，$omega_r$表示反射光角度，函数返回反射光辐射率。$omega$由球面坐标系的$phi$,$theta$角度表示，因此brdf函数共有4个参数。brdf的单位是每立体角$sr^(-1)$。

辐射度量学(Radiometry)

BRDF由Fred Nicodemus在1965年提出，函数如下：

$$f_r(omega_i,omega_r) = (dL_r(omega_r))/(dE_i(omega_i)) = (dL_r(omega_r))/(L_i(omega_i)cos theta_i d omega_i) $$

这个公式之所以定义为辐射率（radiance）和辐照度（irradiance）之比，而不是radiance和radiance之比，或irradiance和irradiance之比。是因为当考虑入射时，我们需要考虑入射光在面积上的分量，所以irradiance译为辐照度。当考虑反射时，我们需要考虑每立体角的辐射通量，并且这个辐射通量最终投影在屏幕（视网膜）面积上的辐射通量，因此我们用辐射率。如果我们用点光源，入射光的计算似乎也是可以用辐射率的，但有时我们还要考虑平行光的情况，那么对于入射光就不存在每立体角的概念了，因此对于入射光照我们用辐照度，反射我们用辐射率。

基于物理的BRDF模型(PBR，Physically-based rendering)

次表面散射（Subsurface scattering）

是一些半透明物质比如皮肤、玉石、大理石、塑料等。当光入射到材料表面后，一部分被反射、一部分被吸收、还有一部分经历透射，透射光在材料内部进行多次不规则的反射之后，又从不同角度反射了回来。

菲涅尔反射（Fresnel Reflectance）

当光从一种折射率为$n_1$的介质向另一种折射率为$n_2$的介质传播时，在两者的交界处可能会同时发生光的反射和折射。菲涅尔方程描述了光波的不同分量被折射和反射的情况，也描述了波反射时的相变。光线会随着我们的观察角度而反射不同的亮度，当我们以垂直与水面的角度观察池塘时，我们可以看到池塘的底部，但当我们以平行于水面的角度观察水面时，反射光则会很强我们无法看到池底。

微表面理论（Microfacet Theory）

微表面理论假设材质的表面是由不同方向的微小细节平面（microfacet）所构成，反射光线由这些微表面的法线分布决定。我们用法线分布函数（Normal Distribution Function，NDF），D(h) 来描述表面的法线分布概率。h表示视角与入射光角度之间的半程向量。

$$f(i,o) = (F(i,h)G(i,o,h)D(h))/(4(n,i)(n,o))$$

其中F(i,h)表示菲涅尔项，表示所有反射的比例。G(i,o,h) 表示自投影项，当光线几乎平射于微表面时，光线则将被粗糙的表面自我遮挡掉。D(h)表示法线分布。

参考:

Wikipedia:《Bidirectional reflectance distribution function》

《Real-Time Rendering, 4th edition》

《Real-Time Rendering 3rd》提炼总结

Microfacet材质和多层材质——文刀秋二

当我在大学中学习线性代数的时候，我不知所云且不以为然。然后随着不断的学习，我发现不懂线性代数是没法在更深的技术领域里混的。比如机器学习、计算机图形学等等，对于其他的科研领域也都是同样的。如果学不好线性代数既不是我的问题，也不是线性代数的问题，那到底是什么问题？最近学些了现代计算机图形学入门-闫令琪 线性代数的本质-3blue1brown 这两个系列视频使我对线性代数多了更多的感性认识，而《实践论》 告诉我们，理性认识是要依赖于感性认识的。传统的线性代数教材则希望构建一套完全自洽的纯粹的数学理论，它不依赖于现实世界的知识。这或许可以满足一些数学家的成就感，但这种马后炮式的“创造”是脱离历史的。线性代数就像其他的学科一样，不可能是仅凭想象产生的，虽然数学家可以伪装成不依赖历史发展而独立自洽，但这除了是一种智力游戏外，对于认识世界、传播知识并没有任何帮助。我们就在这种缺乏感性认识的数学教育中丧失了对数学理论的兴趣，岂不哀哉？

吐槽结束，进入正题。谈谈我此刻对线性代数的理解，探讨一下他的本质到底是什么。我们是否会问自己，加减乘除的本质到底是什么？我们之所以不这么问，是因为我们已经理解了四则运算的本质。我们不会问关于十进制的本质，因为日常生活中已经给我们建立了足够多的经验。但我们在学龄前的阶段，我们则可能对十进制和加减乘除充满了困惑。但我们接触线性代数太晚，我们并没有足够的练习和日常应用使我们建立起感性认识。当我们在商店里消费的时候四则运算不断强化着我们的认知，但线性代数缺少这样的机会。当我们被教授四则运算时，老师把我们当作一个普通的人类，会告诉我们3个苹果+2个苹果=5个苹果，这种现实世界的例子帮助我们更好的理解了四则运算。但当我们学习线性代数时，我们则变成了一个个抽象的理性机器，这个系统只告诉我们各种定义、运算规则，然后要求我们像计算机一样的运行，计算出结果。What are we doing？我们怎么可能不懵圈呢？线性代数就是一个增强版的加减乘除，但没有足够的案例使我们不知道我们的计算究竟代表着什么？AlphaGo就算赢了李世石，但他不知道自己在干什么。我们作为人类的尊严在哪里？我又没控制好自己的情绪，让我们回到正题。《线性代数及其应用》是一本很好的教材，他和国内教材最大的区别就在于“应用”上，这本书中列举了大量的例子来说明线性代数的应用。这本书的开头说道“线性代数是一门语言，必须用学习外语的方法每天学习这种语言”。

鸡兔同笼与线性变换

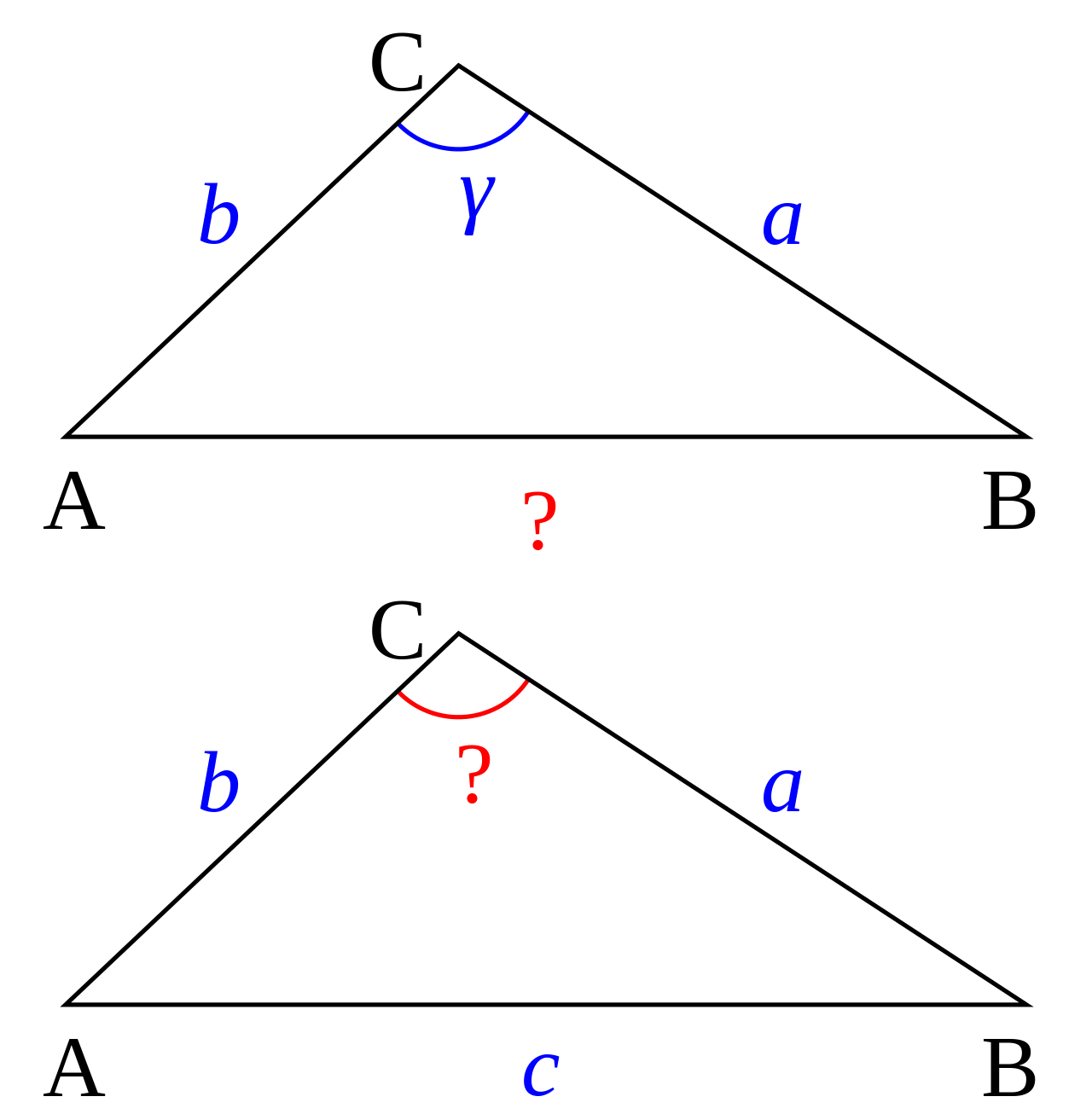
我们从鸡兔同笼来举个例子。鸡兔同笼是小学阶段的奥数题，也就是在小学的数学语言中，这是一道很难描述的题。到了中学阶段我们可以用未知数x表示鸡的数量，未知数y表示兔的数量，并列出方程。而对于线性代数的语言，我们用向量$$((a),(b))$$表示鸡和兔的数量，如果我们有非常多的未知数，我们不希望定义太多的未知数符号，我们直接用$$x$$表示这个n维变量。我们有一个变换矩阵$$[[1,1],[2,4]]$$ 表示鸡有1个头2只脚，兔有1个头4只脚 。如果有3只鸡5只兔则 $$[[1,1],[2,4]]*[[3],[5]]=[[3*1+5*1],[3*2+5*4]]=[[8],[26]]$$，它代表着我们将一个“鸡兔向量”映射到了“头脚向量”的空间中，共有8只头，26只脚。

我们知道函数是一种映射，$$f(x)=y$$代表将$x$到$y$的映射关系。矩阵乘法叫做线性变换，线性变换是一种函数映射，但函数映射不一定是线性变化。因此线性变换是符合函数的性质的。如果函数是可逆的，则有$$x=f^(-1)(y)$$，同样的，对于矩阵而言，$$若A是可逆的，且Ax=b，则x=A^(-1)b。设A=[[a,b],[c,d]]，则A^(-1)=1/(ad-bc)[[d,-b],[-c,a]]$$。

对于鸡兔同笼问题，$$A=[[1,1],[2,4]]，则A^(-1)=1/2[[4,-1],[-2,1]]$$。$$当有8头26脚时，x=1/2[[4,-1],[-2,1]]*[[8],[26]]=1/2[[4*8-26],[-2*8+26]]=1/2[[6],[10]]=[[3],[5]]$$，即3只鸡5只兔。最重要的是，这整个计算过程，计算机可以轻松的完成，并且可以用定义标准化的操作，因为操作标准化，计算机可以被设计的更加擅长处理这类操作。这就是线性代数得到广泛应用的一个最重要原因。

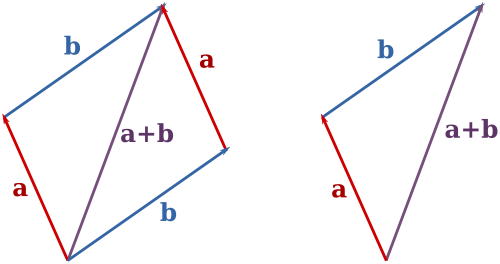
线性变换可能进行多次，就像映射可以进行多次一样。因为矩阵的乘法就是一种特殊的函数，函数满足结合律$$g(f(h(x)))=((g @ f)(h(x)))$$，所以矩阵乘法也符合结合律$$A(BC)=(AB)C$$。多次映射之后是一个新的映射，多次变换之后也是一个新的变换，所以我们可以将这些变换矩阵预先乘好，以增加每次计算的效率。也可以将一个复杂变换拆解为多个简单变换，使我们能更好的理解其性质。

我们可以从鸡兔变换到头脚，我们也可以从产量变换到成本收益（这是经济学的应用），我们也可以从速度变换到阻力（这是空气动力学的应用），我们也可以将3D空间变换到3D或2D空间（这是计算机图形学的应用），我们也可以将用户行为维度变换到兴趣标签维度（这是机器学习推荐系统的应用）。这都说明了线性代数是一门“语言”，是一个工具。并不是因为线性代数，所以这些定理存在，而是因为这些规律本身存在，才能有线性代数这门工具。人类是巧妙的“发明”了线性代数，而不是“发现”了线性代数。线性代数这门语言可以使我们避免基本代数语言的变量名爆炸。人类日常语言中有你我他这那等代词，中文有甲乙丙丁这种天干地支可以用作代词，英文则有a,b,cd可以使用。日常的代词使用是随意的，很多时候是不严谨的。代数学的代词在使用前则需要对它进行准确的定义。而线性代数则将最常使用的一些操作提取了出来，使我们免于重复的定义大量性质类似的代词。在线性代数中，鸡兔数量，头脚数量与空间中点的xyz轴位置都是同一种性质的。研究飞机表面的气流的过程包含了反复求解大型的线性方程组$$Ax=b$$，涉及的变量个数达到2百万个。可以说线性代数的发展完全是随着其应用发展的，如果有一本按照历史发展顺序描述线性代数的书，一定可以达到很好的教学效果。

行列式（determinant）

行列式的出现是远早于矩阵的。Determinant是决定的意思，（下文称之为决定值，“行列式”翻译的无味，既没有描述其决定性质，也没有说明其结果是特定的值）：决定值是否不为0决定了一个线性方程组是否有唯一解。所谓线性方程组，就是一次方程组。这个结论最早见于《九章算术》（有一种观点认为很多思想是在明朝由中国传至欧洲，而清朝恰好是中国的一个倒退，而欧洲则顺势伪造了一套其文明独立发展的历史叙事，这里不展开描述了）。决定值的这个性质在欧洲由莱布尼茨最早提出（莱布尼茨在中学西传中扮演着重要角色）。高斯首先使用了determinant这个词，他在数论理论中大量用到了决定值。后来这个词就更多的指一个特殊的函数，即某个表达式，因此中文将其翻译为行列式。

观察我们在鸡兔同笼中得出的结论：$$设A=[[a,b],[c,d]]，则A^(-1)=1/(ad-bc)[[d,-b],[-c,a]]$$。因此矩阵A当且仅当$$ad-bc!=0$$时存在逆矩阵，我们记为$$det(A)=|A|=|[a,b],[c,d]|=ad-bc$$。我们继续推广研究$3xx3$矩阵，可以得到：

$$|[a,b,c],[d,e,f],[h,i,j]|=a|[e,f],[h,i]|-b|[d,f],[g,i]|+c|[d,e],[g,h]|=aei+bfg+cdh-ceg-bdi-afh=|[a,d,h],[b,e,i],[c,f,j]|$$

对$4xx4$矩阵则有：

$$|[a,b,c,d],[e,f,g,h],[i,j,k,l],[m,n,o,p]|=a|[f,g,h],[j,k,l],[n,o,p]|-b|[e,g,h],[i,k,l],[m,o,p]|+c|[e,f,h],[i,j,l],[m,n,p]|-d|[e,f,g],[i,j,k],[m,n,o]|$$

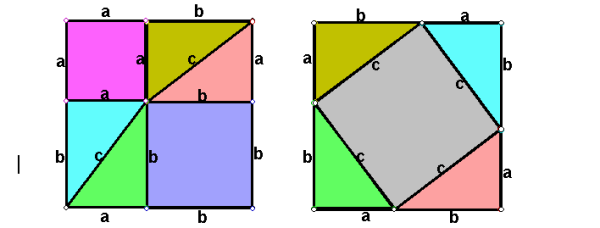
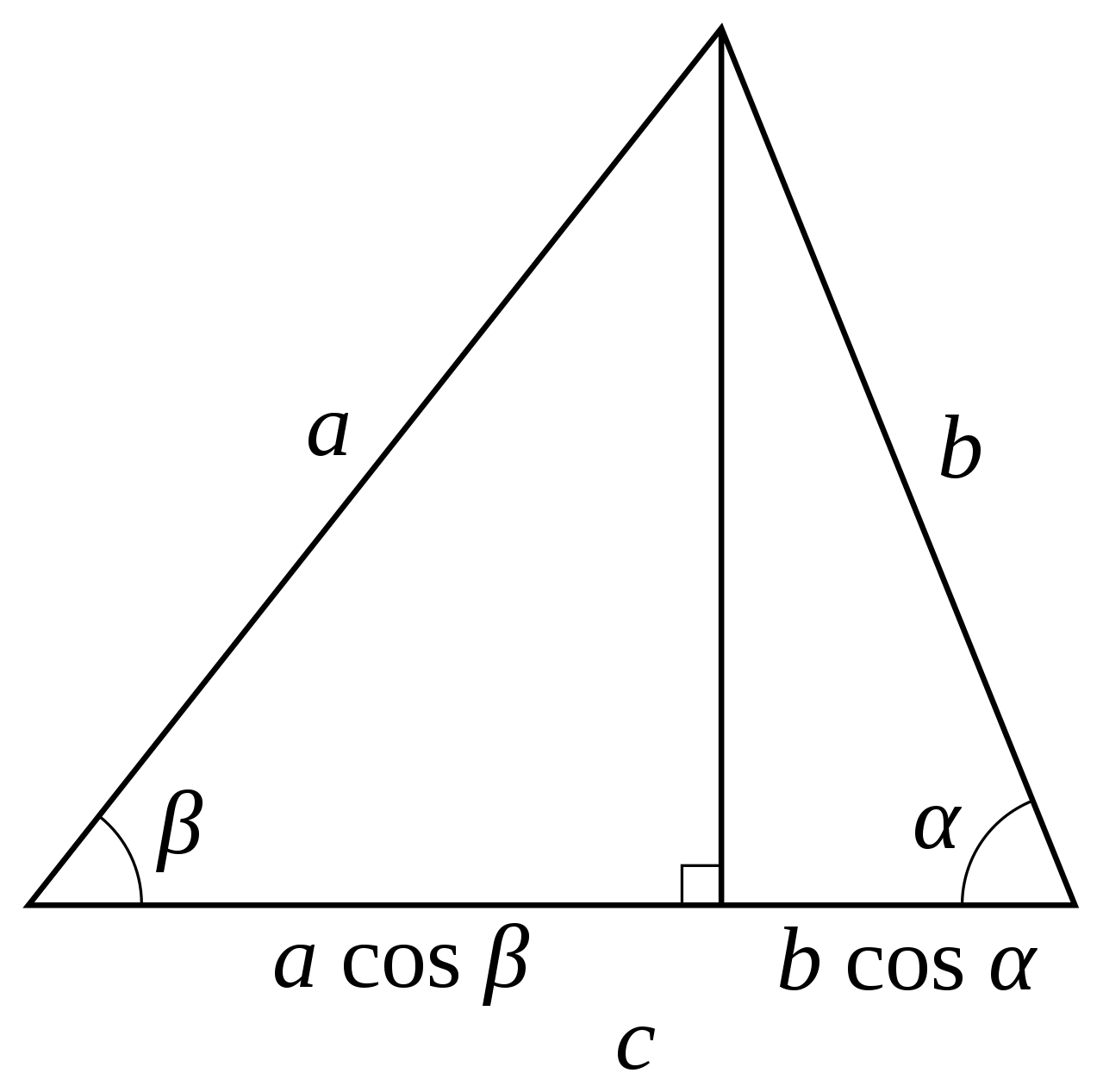
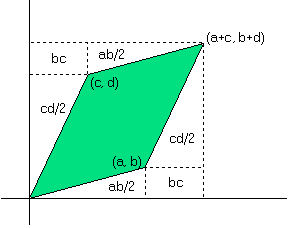
依此类推，决定值的公式是一个递归。决定值的几何意义代表代表$1xx1$矩阵变换后的平行四边形的面积，或者说是矩阵变换后面积的放大倍数，即变换矩阵围成的四边形的面积。简单的证明如下图：$S=(a+c)(b+d)-ab-cd-2bc=ad-bc$。推广到3维则表示变换矩阵的围成的立方体的体积。

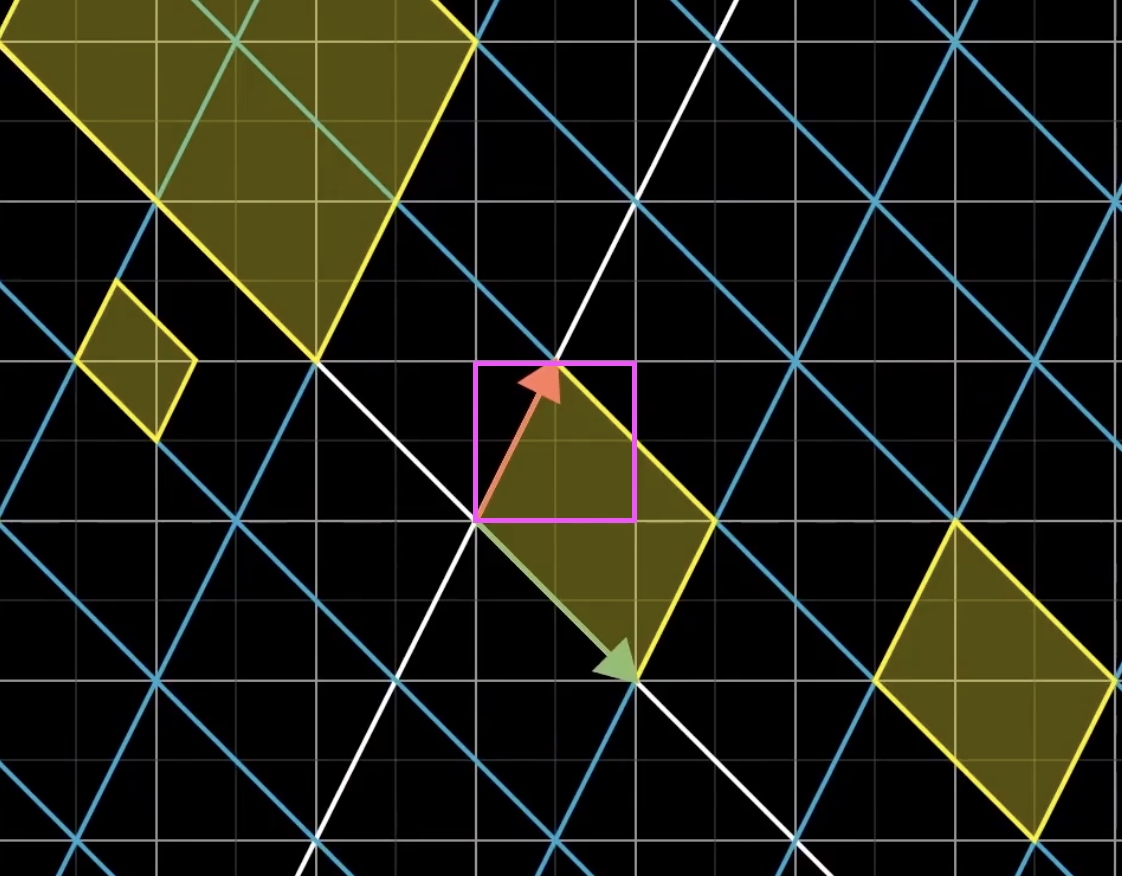
如果determinant=0，则说明变换之后由面变为了线，或由体变为了面。而线或面无法再变换回面或体。我们同样以鸡兔同笼问题来举例，我们把题目中的兔换成鸭，则变换矩阵为$$A=[[1,1],[2,2]], det(A)=0$$。这个方程组是没有唯一解的，因为无论鸡鸭的比例如何，头脚的比例都是$1:2$。对于这样的矩阵，我们称他的秩为1，秩代表矩阵的维数。一个二维矩阵，可能秩为1，一个三维矩阵可能秩为2也就是一个面，也可能秩为1也就是一条线，甚至秩为0。

TODO 叉乘表示面积和垂直与平面的向量，特征值与特征向量，表示空间中在线性变换中保持稳定的轴，最小二乘法

1.勾股定理——宇宙的密码

$a^2+b^2=c^2$。下图是勾股定理的一个直观证明。

2. 余弦定理，角与边的关系

三条边可以确定一个三角形，已知三角形的三条边长，如何求出其角度呢？

由$cos,sin$定义可知
$$ c = a * cos beta + b * cos alpha $$
两边同乘c得：
$$ c^2 = ac * cos beta + bc * cos alpha $$
同理可得：
$$ a^2 = ac cos beta + ab * cos gamma $$
$$ b^2 = bc cos alpha + ab cos gamma $$
故：$$ a^2+b^2-c^2 = 2abcosgamma $$
可得：$$ c^2 = a^2 + b^2 - 2ab cos gamma $$

3. 向量的定义（方向）

$$令 vec c = vec a - vec b$$, $$theta$$为$$vec a$$ $$vec b$$ 的夹角。余弦定理可以用向量形式写成 $$ | vec c |^2 = |vec a|^2 + |vec b|^2 - 2 |vec a| |vec b| cos theta $$

4. 点积（dot product）的代数定义

两个向量的点积是一个标量。向量$$vec a=[a_1, a_2, … a_n]$$与向量$$vec b=[b_1, b_2, … b_n]$$的点积定义为: $$ vec a * vec b = sum_(i=1)^n a_i b_i = a_1 b_1 + a_2 b_2 + … a_n b_n $$。

点积有以下性质（证略）：

1. 满足交换律 $$vec a * vec b = vec b * vec a$$
2. 满足分配律 $$vec a * (vec b + vec c) = vec a * vec b + vec a * vec c$$
3. 乘以标量时满足 $$ (c_1 vec a) * (c_2 vec b) = (c_1 c_2)(vec a * vec b)$$
4. 不满足结合律。因为标量 $$ vec a * vec b $$ 与向量 $$ vec c $$ 的点积没有定义，所以$$(vec a * vec b) * vec c=vec a * (vec b * vec c)$$ 没有意义。

点积的代数定义简单实用，易于表示，也易于使用计算机程序处理。是线性代数的基本操作之一。

5. 点积的几何意义

对于任何一个n维向量有 $|vec a|^2=a_1^2+a_2^2+…+a_n^2$。根据勾股定理，这是很显然的。换个角度说如果没有勾股定理，这一步就不存在，后面的内容也不存在了。而勾股定理不是由代数方法证明的，而是独立于代数系统之外的空间基本性质。而空间和时间是宇宙最根本的本质。这就是勾股定理最神奇的地方。

我们根据点积的定义可知：$$ vec a * vec a = a_1 * a_1 + a_2 * a_2 + … a_n * a_n = |vec a|^2$$ 即 $$ vec a * vec a == |vec a|^2$$

我们根据余弦定理的向量表示可得：$$ vec c * vec c = vec a * vec a + vec b * vec b - 2 |vec a| |vec b| cos theta . (1)$$

根据向量的定义 $$ vec c = vec a - vec b $$ 有 $$ vec c * vec c = (vec a - vec b) * (vec a - vec b) = vec a * vec a + vec b * vec b - 2 vec a * vec b . (2)$$

结合等式$$(1)$$、$$(2)$$有 $$vec a * vec b = |vec a| |vec b| cos theta$$。一个看似简单的代数点积操作，竟然和夹角余弦相关，真是不可思议。

点积的几何意义是什么呢？关键就在这个$cos theta$，如果$$|vec b|$$为1时候，我们可以将$$vec a * vec b$$视为$$vec a $$在$$vec b$$方向上的投影长度。

6. 点积的物理意义（从数学到宇宙）

点积的物理意义就是向量在某方向上的投影长度。这在物理上可以表达力在某方向上的投影，光在某方向的投影，速度、加速度在某方向的投影。而点积的操作，可以使我们只需要关心这些物理量的向量表示，而不需要去关心夹角，不需要去计算三角函数。而在统计学、机器学习等方面，余弦可以表示两个向量之间的相似性，比如两个词向量，两个用户的兴趣向量等，应用非常广泛。下面就以计算机图形学举例来说明点积的应用。

冯氏光照模型将一个物体的光照分解为环境光+漫反射光+镜面反射光。

环境光比较简单就是一个常量。而漫反射光，则为光照强度在平面的法线方向的投影，与法线方向一致则光照最强。镜面反射光则为反射光方向在视角方向上的投影，与视角完全一致，则反射光最强。

OpenGL的shader大致如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

vec3 CalcDirLight(DirLight light, vec3 normal, vec3 viewDir) {
    // normalize 归一化，使法线向量的长度为1
    vec3 lightDir = normalize(-light.direction);
    // 漫反射光. dot 计算cos* 强度， max把负值最多降到0，表示全黑。
    float diff = max(dot(normal, lightDir), 0.0);
    vec3 reflectDir = reflect(-lightDir, normal);
    // dot 计算反射光在视角上的cos分量，至少为0。使用pow，模拟镜面光焦点分布集中度，shininess越高要求反射分量越接近于1
    // 反射分量==1 表示必须视角恰巧与反射角完全一致才能看到反射光，也就是绝对镜面
    float spec = pow(max(dot(viewDir, reflectDir), 0.0), material.shininess);
    // 合并冯氏光照结果
    vec3 ambient = light.ambient * vec3(texture(material.diffuse, TexCoords));
    vec3 diffuse = light.diffuse * diff * vec3(texture(material.diffuse, TexCoords));
    vec3 specular = light.specular * spec * vec3(texture(material.specular, TexCoords));
    return (ambient + diffuse + specular);
}

这是描述一群天启儿童降世后如何夺权的故事。天启之后出生的儿童，虽然未受到天启，但是天启一代已经对他们造成了不可逆的影响。

异象出现的那个夜晚，出生了百万个孩子。这是最近百年来出生人口最多的一天。全球实现城市化已经有一百年了，一百年来人类预期寿命不断增加，人口出生率则不断下降。（此处可展开描写，兼叙历史）

异象五年，一首儿歌在孩子们间流传：『XXX，XXX，XXXXXXX,XXX,XXX,XXXXXXX』言辞似无意义，其中『立约』又似有所指。孩童嬉戏玩闹，皆歌之。孩子们天真无邪，他们似乎并不知道他们的歌中有种可怕的气息。（此处可展开描写）

异象十二年，这一批刚刚进入青春期的孩子，开始制造自己的流行文化。他们用发型、衣着与年长自己的人区隔开。那些仅比他们大一两岁的学长学姐们，也有些人受到了这种文化的影响。那些仍然当红的流行明星，成为了他们嘲笑的对象。A（一个女孩）因为他的鼻子长得像Y（一个明星）而倍感苦恼。这种原本被视为漂亮的鼻型在这群孩子种被视为是不自然的。

从异象十五年开始，高中辍学率不断上升，留在学校的学生也对老师教授的所谓知识毫无兴趣。『科学是暴力的工具，与智慧无关』这种奇怪的反智论调在学生中流传。但这并不意味着这些学生是无知的，他们可以随时从互联网上获取自己想要的知识。『我们要自我教育』一些老师们对于这种危险的口号忧心忡忡又无可奈何，更多的教师则认为这不过是年轻人的躁动，不足为奇。这些学生建立起了自己的P2P社交网络，完全匿名，技术上无法监控。有一些校风颇为严格的学校，直接在非教学时间关闭了供电系统，但这激起了学生们的反抗，让人无法理解的是，反抗的积极分子大多是低年级的学生，而高年级的学生则多是观望的角色。

异象十八年，这一年的一流大学的招生遇到了很大的困难，报考者大多资质平平。这些曾经高高在上的学府对此大惑不解。据一名各项测试成绩平平，却轻松进入一流大学的幸运者称，这是他们刻意为之，目的是把水搅混，把这些名牌大学的牌子搞臭，至于为什么要把这些名牌大学的牌子搞臭，他们并没有说，似乎认为这都是公开的秘密了。而那些成绩优异的人，不过这一届的成绩有多少可信之处呢？而那些被认为聪慧敏捷的，则有目的的『占领』那些中低端的学校，

异象二十年的选美结果出炉了，令富豪们大跌眼镜。现在的正常的年轻人，有几个人会参加上一代人创建的选美比赛呢？今年又有几家面向年轻人的时尚公司倒闭了，他们完全搞不明白这些年轻人想要穿什么，似乎他们的设计总是完美的避开了年轻人的审美。这些年轻人总是穿着一些不知名的小品牌的服装，他们甚至以穿着旧衣服、与他人交换服装为时尚。这简直就是要他们的命。『天下皆知美之为美，斯恶矣』一位蓬头垢面，衣着污秽的艺术家如是对记者说。

异象二十二年，一年比一年差的就业形势，到了这一年跌倒了最低点。虽然很多的岗位都已经用机器人代替了人工，但『精英企业家』们依然为了『社会公益』而『创造了大量的就业岗位』。与异象前二十年的人们不同，这届人民似乎丝毫不懂得什么叫做『感恩之心』，若没有他们『创造』出如此多的就业岗位，他们的父母怎么可能有能力供养他们长大。每念及此，年近一百二十岁的企业家老李就倍感痛心。『我还能为社会再干30年』他面对镜头时既谦逊又绅士。

（TODO）

人类在数万年前进入了一个新的状态，太初之人，完满自足，而后散布天下。

庄子天下篇说，上古之人真是完备啊，可惜后世的人很不幸，他们将看到道术在天下分裂。

古希腊哲学、古印度思想、中国古代思想，有一个更统一的源头。那就是上古太初之人。

我们今天的思想是东西方思想的结合，依然不够完满，缺失了重要的部分。

美洲文化受到了破坏。非洲有一部分上古文化留存，苗瑶族也有一些上古之道留存。但都不完整。

我们的目标应该是恢复一个人类上古之道，而不是自称独立发展的，自绝于世界。

也不是盲目的学习他人，放弃自己，因为他人也不过是缺憾的存在。

人类无论从基因上，还是从思想上，都是残缺的。

我们需要追求圆满自足，这是人所遗忘的功能。

近日尝试使用强化学习解决8x8大小的2048游戏。游戏环境是一个8x8的方格，环境每回合随机生成2个方块，方块的值为2或4，AI的决策空间是上、下、左、右四个操作，所有方块都将向所指示的方向堆叠，如果两个相邻的值相同方块在堆叠方向挤压，则这两个方块合并为1个方块，值是两个方块值的和。如果任何方向都无法移动方块，则游戏结束。游戏的目标是尽可能久的玩下去，合并出最大的方块。

最初我尝试用PG来训练这个看似简单的游戏。每一步，都视为1点奖励，如果失败则给予-1000惩罚。算法很快习得了一个偷懒的方法，每一步都进行无效的移动，以此来苟延残喘。于是将无效的移动操作，视为重大的失误，也同样给予-1000的惩罚。算法很快学会了在一个局面下的有效移动操作。但这个游戏，哪怕只是随机的移动也能够取得一个普通的结果，如果要突破极限，则需要使用一些特殊的策略，我期待算法是否能在训练中学会这些策略。

对于这个游戏，达到2048，需要大约500次移动，达到4096，则需要1000，达到1M，也就大约需要20多万次移动，达到4M，则需要上百万次移动。每到达一个新的难度，面临的局面都不同，之前所习得的经验就不一定继续有效了。2048游戏是一个比围棋要简单很多的游戏，围棋拥有更多的选点，2048只有4个操作选择。他们的主要区别在于围棋一般在100多手内结束，而2048的游戏时间则近乎无限长。理想的游戏结果如下图所示：

这一游戏是存在理想玩法的，经过很多局的游戏，我已总结出一些经验。但是这些经验是感性的，很难使用逻辑规则表达出来，很多时候是凭直觉的。我手段操作达到了512K的结果，虽然我依然可以挑战更高的游戏记录，但显然我不能将如此多的时间浪费在滑动手指上。这也是我要编程解决这个问题的初衷，但是强化学习算法，只能在一次次的失败中得到教训，可是这个游戏的特点是，训练的越好，游戏时间越长，获得失败经验的成本就越大。所以无论该算法在理论上是多么的正确，但在实际操作过程中已经变得不可行了。

DQN、PG等强化学习算法的基本过程是根据系统给予的奖励，努力最大化收益。但是对于一个没有明确获胜终点的系统，如果验证训练结果的有效性却是一个非常大的问题。由于强化学习本质上是通过过往的经验来调整自己的策略的，如果有明显的获胜路径，则算法可以有充分的胜利经验可供借鉴。但如果目标是永远安全的运行下去，没有获胜的路径，只有失败的惩罚，那么算法只能在有限的教训中得到学习。假设我们正在训练一个自动飞行系统，获取每一个经验教训的成本都非常巨大，强化学习在这一方面的应用，必须要搭配一些人类的理性评估作为辅助，但是将人类的意识转化为可以实施的程序逻辑又是非常复杂的事情。

如果我们训练的是一个自动驾驶系统呢？在未来无人驾驶会应用的越来越多。无人驾驶的安全性会很快超越人类，随即人们期望可以进一步提升驾驶的平均速度或其他一些智能驾驶的指标。因为无人驾驶的安全性已经超越了人类，所以无法再依赖于人类的驾驶经验给予其帮助，只能依赖于自身驾驶中的经验（尤其是事故）作为训练依据。那么这时这个系统还可能是安全的吗？

在未来的相关强化学习领域，一个好的环境模拟系统、事故全息信息的采集和共享系统，才是提升人工智能的关键，而不是算法。

勤劳致富、知识改变命运，这在很多年里是人的信条。

如果说中国的贫富差距问题，都是政府的问题，我觉得是不恰当的，中国的贫富差距深层次的原因在于民众的思想。大众在思想上并没有真正的完成社会主义改造，很多人只是迫于形势暂时屈从于社会主义集体思想，但本质上并没有放弃发家致富的思想。依然是用私欲在驱使自己，与那些真正拥有共产主义理想甚至愿意为之献生的人是完全不可以相提并论的。这种思想的不同自然会导致经济制度的不同。

资本主义本质上是一种达尔文主义，也就是物竞天择、适者生存的那一套说辞。其漏洞是把人作为独立个体看待忽略了人的社会性，也忽略了人的思想是可以改变的而基因只能突变这种本质区别，这些本质的区别使达尔文的生物进化过程不能够直接的套用于人类的思想演化过程。生物只能依靠随机的不可控的突变来进化，但是人类可以在伟大的哲人带领下通过思辩来改造大众的思想进而改变社会制度。

历史已经证明，只要一种思想能够被普遍的接受哪怕是错误的思想，都会引起社会巨大的改变，比如各种有神论的宗教。而有些思想即便他是更加正确的，只要不能够被大众接受，也就依然无济于事，比如墨子的思想。孟子曾经说过，杨朱和墨翟两个人的言论充斥天下，天下人要么信奉杨朱的思想，要么信奉墨翟的思想。孟子还说：杨朱为我，是无君也，墨翟兼爱，是无父也，无君无父，是禽兽也。杨朱是讲利己主义的，如果拔他小腿上的一根毛能够有利于天下的话，他也不会拔。杨朱这个人留下的话不多，主要是其他诸子骂了他，所以他有些话留了下来，很明显当时是个显学。列子杨朱篇上记载，有人问，做人干嘛要求名呢？杨朱说：求名为了富。又问：已经富了，为什么还不停止呢？答：为贵。又问：已经贵了，为什么不停止？答：为死。（可能是指为了厚葬）。又问：已经死了还为什么呢？答：为子孙。各位看看，杨朱的思想是不是符合世界上大多数人的想法呢？尤其是当代的中国人，所以诸子们没有不鄙视杨朱的。国人以前比较贫穷，有些人因为贫穷而自卑，以为富起来就会受人尊重，但是最后发现，富起来之后，人家照样瞧不起你。为什么呢？这个问题是值得思考的。有些人则不同，即使贫穷却依然受到全世界的尊敬，比如墨子。

除了孟子骂过墨子，其他人都是尊敬墨子的。我想孟子也不是要骂墨子，而是为了捍卫儒家思想不得已的反击，因为墨子反对礼乐，反对亲疏贵贱。但事实上儒家和墨家有很多共同的价值观，儒家大同社会的理想和墨家思想几乎没什么区别“大道之行也，天下为公。选贤与能，讲信修睦。故人不独亲其亲，不独子其子……是谓『大同』。”，“今大道既隐，天下为家。各亲其亲，各子其子；……是谓『小康』”。这些话是什么意思呢？意思是不是我们不喜欢墨家，而是墨家实现不了，我们只能暂时降低一下要求，追求小康。所以说儒家是一个妥协的理论，但妥协多了，就会出问题。那些读书人，一旦飞黄腾达了，就过上了“精英”的生活，哪里还会有什么大同的理想呢？妥协只能让不合理的制度继续存在下去，直到达到社会承受的极限才会发生革命。当然儒家也是支持汤武革命的。所以儒家思想是既妥协又革命的，这样究竟好不好，这个我们可以讨论。

墨子认为，你要爱你的父母，最好也爱别人的父母，那么别人也会爱你的父母，这样就可以交相利，兼相爱。有些人是认为人都是怎样的，所以我也要怎样。而墨子认为这样更好，所以你应该这样。比如墨子也有天志明鬼的思想，教人信鬼神，墨子是怎么证明的呢？墨子认为人如果信鬼神的话，会有所敬畏，行善去恶，还能联络感情，加强团结。依然是认为信鬼神更好，所以人应该信奉鬼神。墨子的思想都是从对整个社会更有利的角度去分析，然后认为人应该是什么思想的。因为墨子的思想逻辑严谨，加上墨子本人身体力行，所以墨子的门徒全都是信仰坚定，赴汤蹈火，死不旋踵。墨子的组织是可以存在的，但这种组织的存在建立在墨家的共同信仰基础上，如果没有这种共同信仰，这种组织也就无法存在了。简而言之，你相信，他就会实现，你不相信，他就不会实现。庄子天下篇评价墨子，“其生也勤，其死也薄，其道大觳，使人忧，使人悲，其行难为也，恐其不可以为圣人之道，反天下之心，天下不堪。墨子虽能独任，奈天下何！”。他认为，墨子的道太惊人了，使人担忧，又使人悲哀，与天下人的想法都是相反的，墨子你虽然能吃得了那些苦，对天下又有什么办法呢？

庄子的评价不是没有道理，天下人不信墨子，害怕受墨子之苦，那么天下人的结局是什么呢？不受墨子之苦，就要受秦法之苦。商君有法，墨子也有法。商鞅的法是等级制，墨子的法是平均制、供给制。（引用一个故事：墨者巨子腹，居秦，其子杀人。惠王曰：‘先生年长矣，非有他子也，寡人已令吏勿诛矣。’腹对曰：‘墨者之法，杀人者死，伤人者刑，王虽为赐，腹不可不行墨者之法。’遂杀其子） 商鞅和墨子没有能够相互辩论，但是曾经有两位湖南人就此事发生过巨大的分歧。

人们没有选择墨子之法，选择了商君之法，秦国一统六国。对商君之法不满意，高祖斩白蛇而起义。汉初信奉道家的自由主义，自由主义导致豪族逐渐产生，国力削弱。汉武帝随后又开始拿出妥协的儒家，无论是举孝廉还是九品中正，还是科举，但依然向着门阀社会不可逆转的滑落了下去，虽有赤眉起义、黄巾起义依然不能阻止。然后是五胡乱华，几乎是亡国灭种。按照天下人心自然发展下去，结果就是如此。西晋的石崇富可敌国，名士王导和王敦去他家作客，石崇让美人劝酒，如果客人不喝，石崇就会杀掉美人。王敦根本不管这一套，就是不喝，石崇连杀了三个美人，他仍然不喝。王导责备王敦，王敦说：“他杀他家的人，和你有什么关系？”人已经彻底沦为了奴隶，成了某些人的私有财产，而这些知识分子也对此是无动于衷的。

墨子被人遗忘了很多很多年，统治者绝对不会提起墨子。商君之法和儒家的妥协，可以保证社会稳定几百年，然后再重来一次。天下人总是不愿意放弃自己的幻想，以为自己有一天也可以王侯将相，或者如石崇富可敌国，抑或如王谢名士风流，只有发现权、利、名都与自己无关时，依然不能醒悟。其实他们不知道，就算是石崇等人，也都没有什么善终，为什么还要抱这种幻想呢？无论是举孝廉还是科举制，无论提供怎样的晋升阶梯，这种旧制度的修修补补都进一步延长了这种旧制度。直到一场全球范围的更大的战国乱世出现，才有人提出了和墨子类似的主张，那就是共产国际。但是，只要天下人心未变，墨子之道，就永远没有实现的一天，人类就必须困在相互倾轧的循环中万劫不复。

因为智齿不影响自然选择，所以智齿会一直存在于人的口中。那么和智齿一样，还有很多的特征也伴随着人类的演化流传了下来。

人为装饰越多，问题越多。人为装饰导致一个错误的基因得到了遗传。

天启宗教是现代文明的伴生文化。

现在继承中国传统文化，你继承和恢复的可能不是中华文化，而是中华文化的伴生文化。