近日尝试使用强化学习解决8x8大小的2048游戏。游戏环境是一个8x8的方格，环境每回合随机生成2个方块，方块的值为2或4，AI的决策空间是上、下、左、右四个操作，所有方块都将向所指示的方向堆叠，如果两个相邻的值相同方块在堆叠方向挤压，则这两个方块合并为1个方块，值是两个方块值的和。如果任何方向都无法移动方块，则游戏结束。游戏的目标是尽可能久的玩下去，合并出最大的方块。

最初我尝试用PG来训练这个看似简单的游戏。每一步，都视为1点奖励，如果失败则给予-1000惩罚。算法很快习得了一个偷懒的方法，每一步都进行无效的移动，以此来苟延残喘。于是将无效的移动操作，视为重大的失误，也同样给予-1000的惩罚。算法很快学会了在一个局面下的有效移动操作。但这个游戏，哪怕只是随机的移动也能够取得一个普通的结果，如果要突破极限，则需要使用一些特殊的策略，我期待算法是否能在训练中学会这些策略。

对于这个游戏，达到2048，需要大约500次移动，达到4096，则需要1000，达到1M，也就大约需要20多万次移动，达到4M，则需要上百万次移动。每到达一个新的难度，面临的局面都不同，之前所习得的经验就不一定继续有效了。2048游戏是一个比围棋要简单很多的游戏，围棋拥有更多的选点，2048只有4个操作选择。他们的主要区别在于围棋一般在100多手内结束，而2048的游戏时间则近乎无限长。理想的游戏结果如下图所示：

这一游戏是存在理想玩法的，经过很多局的游戏，我已总结出一些经验。但是这些经验是感性的，很难使用逻辑规则表达出来，很多时候是凭直觉的。我手段操作达到了512K的结果，虽然我依然可以挑战更高的游戏记录，但显然我不能将如此多的时间浪费在滑动手指上。这也是我要编程解决这个问题的初衷，但是强化学习算法，只能在一次次的失败中得到教训，可是这个游戏的特点是，训练的越好，游戏时间越长，获得失败经验的成本就越大。所以无论该算法在理论上是多么的正确，但在实际操作过程中已经变得不可行了。

DQN、PG等强化学习算法的基本过程是根据系统给予的奖励，努力最大化收益。但是对于一个没有明确获胜终点的系统，如果验证训练结果的有效性却是一个非常大的问题。由于强化学习本质上是通过过往的经验来调整自己的策略的，如果有明显的获胜路径，则算法可以有充分的胜利经验可供借鉴。但如果目标是永远安全的运行下去，没有获胜的路径，只有失败的惩罚，那么算法只能在有限的教训中得到学习。假设我们正在训练一个自动飞行系统，获取每一个经验教训的成本都非常巨大，强化学习在这一方面的应用，必须要搭配一些人类的理性评估作为辅助，但是将人类的意识转化为可以实施的程序逻辑又是非常复杂的事情。

如果我们训练的是一个自动驾驶系统呢？在未来无人驾驶会应用的越来越多。无人驾驶的安全性会很快超越人类，随即人们期望可以进一步提升驾驶的平均速度或其他一些智能驾驶的指标。因为无人驾驶的安全性已经超越了人类，所以无法再依赖于人类的驾驶经验给予其帮助，只能依赖于自身驾驶中的经验（尤其是事故）作为训练依据。那么这时这个系统还可能是安全的吗？

在未来的相关强化学习领域，一个好的环境模拟系统、事故全息信息的采集和共享系统，才是提升人工智能的关键，而不是算法。

和第四节DQN的实例一样，我们依然使用CartPole-v1来作为训练环境。策略梯度的网络和DQN的网络结构是类似的，只是在输出层需要做Softmax处理，因为策略梯度的输出本质上是一个分类问题——将某一个状态分类到某一个动作的概率。而DQN网络则是一个回归问题——某一个网络在各个动作的Q值是多少。

1
2
3
4
5
6
7
8
9
10
11

class PolicyNet(nn.Module):
    def __init__(self, input_size, hidden, outputs):
        super(PolicyNet, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden)
        self.fc2 = nn.Linear(hidden, outputs)

    def forward(self, x):
        x = F.relu(F.dropout(self.fc1(x), 0.1))
        x = self.fc2(x)
        # 输出层需要使用softmax
        return F.softmax(x, dim=1)

不要忘了输出层的SoftMax。

初始化参数

相对于DQN，我们也不需要额外的目标网络和参数复制操作，只需要一个策略网络即可。

1
2
3
4
5
6
7
8
9
10
11
12

BATCH_SIZE = 256
GAMMA = 0.99
HIDDEN_SIZE = 15
LR = 0.005

n_actions = env.action_space.n
input_size = env.observation_space.shape[0]

policy_net = PolicyNet(input_size, HIDDEN_SIZE, n_actions)
optimizer = optim.Adam(policy_net.parameters(), lr=LR)

steps_done = 0

选择动作

在选择动作时，我们不再需要特地设置探索概率，因为输出结果就是各个动作的概率分布。我们使用torch.distributions.categorical.Categorical 来进行取样。在每次选择动作时，我们同时记录对应的概率，以便后续使用。这个概率就是 `ln pi_theta(S_t,A_t)`

1
2
3
4
5
6
7
8
9
10
11
12

log_probs = []
rewards = []

def select_action(state):
    x = torch.unsqueeze(torch.FloatTensor(state),0)
    probs = policy_net(x)
    c = Categorical(probs)
    action = c.sample()
    # log action probs to plt
    prob = c.log_prob(action)
    log_probs.append(prob)
    return action

优化模型

为了更新参数，我们首先需要计算`v_t`，这在后续参数迭代中需要用到。

• ` v_t = r_(t+1) + gamma * v_(t+1) `

在模拟执行的时候，我们记录了每一步的reward，我们需要计算每一步的`v_t`，其顺序与执行顺序一致。根据公式我们需要倒序的计算`v_t`，然后将计算好的结果倒序排列，就形成了`v_1,v_2…v_t`的序列。最后我们需要将数据标准化。(TODO: 这里可能存在一个序列对应的问题，其中每一个状态的累计收益，是后续状态收益之和，不包含本轮收益)

1
2
3
4
5
6
7
8
9

values = []
v = 0
for reward in reversed(rewards):
    v = v * GAMMA + reward
    values.insert(0, v)
mean = np.mean(values)
std = np.std(values)
for i in range(size):
    values[i] = (values[i] - mean) / std

接下来我们需要更新参数，参数更新的公式为：

• ` theta larr theta + alpha v_t ln pi_theta (A_t|S_t) `

我们将其转换为损失函数形式:

• ` L(theta) = - v_t ln pi_theta(A_t|S_t) `

这个损失函数的形式可以帮助我们更好的理解策略梯度的原理。如果一个动作价值为负值，但是其选择概率为正，则损失较大。

1
2
3
4
5
6
7
8
9
10

loss = []
for i in np.random.choice(size, n):
    loss.append(- values[i] * log_probs[i])
loss = torch.cat(loss).sum()

optimizer.zero_grad()
loss.backward()
for param in policy_net.parameters():
    param.grad.data.clamp_(-1, 1)
optimizer.step()

训练循环

训练循环需要在一局结束之后进行。并清除rewards、log_probs缓存。对于cartpole-v1环境，要注意他的每一步奖励都是1，很显然在最后一步代表着游戏失败，我们需要施加一定的惩罚，我们将最后一步的奖励设为-100。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

num_episodes = 5000
for i_episode in range(num_episodes):
    state = env.reset()
    for t in count():
        action = select_action(state)
        if i_episode % 2000 == 0:
            env.render()
        next_state, reward, done,_ = env.step(action.item())
        if done:
            reward = -100
        rewards.append(reward)
        state = next_state
        if done or t >= 2500:
            optimize_model()
            print('EP', i_episode)
            episode_durations.append(t+1)
            plot_durations()
            rewards = []
            log_probs = []
            break

完整代码

DQN证明了深度学习在增强学习中的可行性。深度学习可以将复杂的概念隐含在网络之中。但是DQN并没有将所有的概念都隐含在网络之中，只是把Q值的计算放在了网络之中，比如`epsilon-greedy`动作选择策略。因为如何选择动作和如何通过Q值计算出目标值，都是DQN所面临的问题，而Q值的目的也是为了选择动作。我们可以将增加学习的问题简化为选择动作的问题。那么我们可否使用深度学习直接做出动作选择呢？显然，我们可以定义一个网络`pi_theta`，其中输入为状态`s`，输出为每个动作`a`的概率。

因为这个网络与策略函数的定义一样，所以被称为策略网络。`pi_theta(a|s)`，表示在`s`状态下选择动作`a`的概率。只要这个网络能够收敛，我们就可以直接得到最佳策略。这个网络的奖励函数也就是最终游戏的总奖励。

`J(theta) = sum_(s in S)d^pi(s)V^pi(s) = sum_(s in S)d^pi(s)sum_(a in A)pi_theta(a|s)Q^pi(s, a)`

`d^pi(s)`指状态`s`在马尔科夫链上的稳定分布，`d^pi(s) = lim_(t->oo)P(s_t=s|s_0,pi_theta)`。

但是这个表达式看上去是不可能计算的，因为状态的分布和Q值都是随着策略的更新而不断变化的。但是我们并不需要计算`J(theta)`，在梯度下降法中我们只需要计算梯度`grad_(theta)J(theta)`即可

`grad_(theta)V^pi(s)`
`= grad_(theta)(sum_(a in A)pi_theta(a|s)Q^pi(s, a))`
根据导数乘法规则
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)grad_thetaQ^pi(s, a))`
展开`Q^pi(s,a)`为各各种可能的下一状态奖励之和
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)grad_(theta)sum_(s’,r)P(s’,r|s,a)(r+V^pi(s’)))`
而其中状态转移函数`P(s’,r|s,a)`、奖励`r`由环境决定，与`grad_theta`无关，所以
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)sum_(s’,r)P(s’,r|s,a)grad_(theta)V^pi(s’))`
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)sum_(s’)P(s’|s,a)grad_(theta)V^pi(s’))`

现在我们有了一个形式非常好的递归表达式：
`grad_(theta)V^pi(s) = sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)sum_(s’)P(s’|s,a)grad_(theta)V^pi(s’))`

设 `rho^pi(s->x, k)` 表示在策略`pi^theta`下，`k`步以后状态`s`转移到状态`x`的概率。有：

• `rho^pi(s->s, k=0)=1`
• `rho^pi(s->s’, k=1)=sum_(a)pi_(theta)(a|s)P(s’|s,a)`
• `rho^pi(s->x, k+1) = sum_(s’)rho^pi(s->s’, k)rho^pi(s’->x, 1)`

为了简化计算，令 `phi(s)=sum_(a in A)grad_(theta)pi_theta(a|s)Q^pi(s,a)`

`grad_(theta)V^pi(s)`
`= phi(s) + sum_(a in A)pi_(theta)(a|s)sum_(s’)P(s’|s,a)grad_(theta)V^pi(s’) `
`= phi(s) + sum_(s’)sum_(a in A)pi_(theta)(a|s)P(s’|s,a)grad_(theta)V^pi(s’) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)grad_(theta)V^pi(s’) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)(phi(s’) + sum_(s’’)rho^pi(s’->s’’,1)grad_(theta)V^pi(s’’)) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)phi(s’) + sum_(s’’)rho^pi(s->s’’,2)grad_(theta)V^pi(s’’) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)phi(s’) + sum_(s’’)rho^pi(s->s’’,2)phi(s’’) + sum_(s’’’)rho^pi(s->s’’’,3)grad_(theta)V^pi(s’’’) `
`= …`
`= sum_(x in S)sum_(k=0)^(oo)rho^pi(s->x, k)phi(x)`

令 `eta(s)=sum_(k=0)^(oo)rho^pi(s_0->s, k)`

`grad_(theta)J(theta)=grad_(theta)V^pi(s_0)`
`= sum_(s)sum_(k=0)^(oo)rho^pi(s_0->s,k)phi(s)`
`= sum_(s)eta(s)phi(s)`
`= (sum_(s)eta(s))sum_(s)((eta(s))/(sum_(s)eta(s)))phi(s)`
因 `sum_(s)eta(s)` 属于常数，对于求梯度而言常数可以忽略。
`prop sum_(s)((eta(s))/(sum_(s)eta(s)))phi(s)`
因 `eta(s)/(sum_(s)eta(s))`表示`s`的稳定分布
`= sum_(s)d^pi(s)sum_a grad_(theta)pi_(theta)(a|s)Q^pi(s,a)`
`= sum_(s)d^pi(s)sum_a pi_(theta)(a|s)Q^pi(s,a)(grad_(theta)pi_(theta)(a|s))/(pi_(theta)(a|s))`
因 ` (ln x)’ = 1/x `
`= Err_pi[Q^pi(s,a)grad_theta ln pi_theta(a|s)]`

所以得出策略梯度最重要的定理：

` grad_(theta)J(theta)=Err_pi[Q^pi(s,a)grad_theta ln pi_theta(a|s)] `

其中的`Q^pi(s,a)`也就是状态s的累计收益，可以在一次完整的动作轨迹中累计计算得出。

算法描述

该算法被称为 REINFORCE

• 随机初始化`theta`
• 生成一个完整的策略`pi_theta`的轨迹: `S1,A1,R2,S2,A2,…,ST`。
• For t=1, 2, … , T-1:
  • ` v_t = sum_(i=0)^(oo) gamma^i R_(t+i+1) `
  • ` theta larr theta + alpha v_t ln pi_theta (A_t|S_t) `

参考：
Lilian Weng:Policy Gradient Algorithms

我们在上文简述了DQN算法。此文以PyTorch来实现一个DQN的例子。我们的环境选用CartPole-v1。我们的输入是一幅图片，动作是施加一个向左向右的力量，我们需要尽可能的保持木棍的平衡。

对于这个环境，尝试了很多次，总是不能达到很好的效果，一度怀疑自己的代码写的有问题。后来仔细看了这个环境的奖励，是每一帧返回奖励1，哪怕是最后一帧也是返回1 的奖励。这里很明显是不合理的俄。我们需要重新定义这个奖励函数，也就是在游戏结束的时候，给一个比较大的惩罚，r=-100。很快可以达到收敛。

Replay Memory

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))

class ReplayMemory:
    def __init__(self, capacity):
        self.cap = capacity
        self.mem = []
        self.pos = 0

    def push(self, *args):
        """Save a transition."""
        if len(self.mem) < self.cap:
            self.mem.append(None)
        self.mem[self.pos] = Transition(*args)
        self.pos = (self.pos + 1) % self.cap

    def sample(self, batch_size):
        return random.sample(self.mem, batch_size)

    def __len__(self):
        return len(self.mem)

Q网络

1
2
3
4
5
6
7
8
9
10

class DQN(nn.Module):
    def __init__(self, input_size, hidden, outputs):
        super(DQN, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden)
        self.fc2 = nn.Linear(hidden, outputs)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

初始化参数和状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import gym

env = gym.make('CartPole-v0').unwrapped

BATCH_SIZE = 128
GAMMA = 0.9
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 200
TARGET_UPDATE = 10
LR = 0.01

n_actions = env.action_space.n
input_size = env.observation_space.shape[0]

# 策略网络
policy_net = DQN(input_size, 10, n_actions)
# 目标网络
target_net = DQN(input_size, 10, n_actions)
# 目标网络从策略网络复制参数
target_net.load_state_dict(policy_net.state_dict())
target_net.eval()

optimizer = optim.Adam(policy_net.parameters(), lr=LR)
memory = ReplayMemory(10000)

探索和选择最佳动作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

steps_done = 0

def select_action(state, no_explore=False):
    x = torch.unsqueeze(torch.FloatTensor(state), 0)
    global steps_done
    sample = random.random()
    eps_threshold = EPS_END + (EPS_START - EPS_END) * math.exp(-1. * steps_done / EPS_DECAY)
    steps_done += 1
    if sample > eps_threshold or no_explore:
        with torch.no_grad():
            # t.max(1) will return largest column value of each row.
            # second column on max result is index of where max element was
            # found, so we pick action with the larger expected reward.
            return policy_net(x).max(1)[1].view(1, 1)
    else:
        return torch.tensor([[random.randrange(n_actions)]], dtype=torch.long)

优化模型(关键代码)

这里主要是抽样、目标值计算、损失计算的部分。损失计算采用Huber loss。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def optimize_model():
    if len(memory) < BATCH_SIZE:
        return
    transitions = memory.sample(BATCH_SIZE)
    batch = Transition(*zip(*transitions))
    non_final_mask = torch.tensor(tuple(map(lambda  s: s is not None,
                        batch.next_state)), dtype=torch.uint8)
    non_final_next_states = torch.FloatTensor([s for s in batch.next_state if s is not None])
    state_batch = torch.FloatTensor(batch.state)
    action_batch = torch.cat(batch.action)
    reward_batch = torch.FloatTensor(batch.reward)
    state_action_values = policy_net(state_batch).gather(1, action_batch)
    next_state_values = torch.zeros(BATCH_SIZE)
    next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
    expected_state_action_values = (next_state_values * GAMMA) + reward_batch

    loss = F.mse_loss(state_action_values, expected_state_action_values.unsqueeze(1))

    optimizer.zero_grad()
    loss.backward()
    # 限制网络更新的幅度，可以大幅提升训练的效果。
    for param in policy_net.parameters():
        param.grad.data.clamp_(-1, 1)
    optimizer.step()

训练循环

这里主要有主循环、获取输入、记录回放、训练、复制参数等环节。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

num_episodes = 1000
for i_episode in range(num_episodes):
    state = env.reset()
    for t in count():
        action = select_action(state, i_episode%50==0)
        if(i_episode%50==0):
            env.render()
        next_state, reward,done,_ = env.step(action.item())
        # reward = torch.tensor([reward])
        if done:
            reward = -100
        memory.push(state, action, next_state, reward)
        state = next_state
        if done or t > 2500:
            for i in range(10):
                optimize_model()
            episode_durations.append(t+1)
            plot_durations()
            break
    if i_episode % TARGET_UPDATE == 0:
        target_net.load_state_dict(policy_net.state_dict())

完整代码

上一个例子中我们使用了冰面滑行的游戏环境，这是一个有限状态空间的环境。如果我们现在面对的是一个接近无限的状态空间呢？比如围棋，比如非离散型的问题。我们无法使用一个有限的Q表来存储所有Q值，即使有足够的存储空间，也没有足够的计算资源来遍历所有的状态空间。对于这一类问题，深度学习就有了施展的空间了。

Q表存储着状态s和动作a、奖励r的信息。我们知道深度神经网络，也具有存储信息的能力。DQN算法就是将Q-table存储结构替换为神经网络来存储信息。我们定义神经网络`f(s, w) ~~ Q(s)`，输出为一个向量`[Q(s, a_1), Q(s, a_2), Q(s, a_3), …, Q(s, a_n)]`。经过这样的改造，我们就可以用Q-learing的算法思路来解决更复杂的状态空间的问题了。我们可以通过下面两张图来对比Q-learning和DQN的异同。

网络结构要根据具体问题来设计。在神经网络训练的过程中，损失函数是关键。我们采用MSE来计算error。

`L(w) = (ubrace(r + argmax_aQ(s’, a’))_(目标值) - ubrace(Q(s, a))_(预测值))^2`

基本算法描述

1
2
3
4
5
6
7
8
9
10
11

使用随机参数初始化网络Q
while 未收敛:
  action 按一定概率随机选取，其余使用argmax Q(s)选取
  模拟执行 action 获取 状态 s_, 奖励 r, 是否完成 done
  if done:
    target = r
  else:
    target = r + gamma * argmax Q(s_)
  loss = MSE(target, Q(s, a))
  使用loss更新网络Q
  s = s_

但是，通过实验我们会发现，训练过程非常的不稳定。稳定性是强化学习所面临的主要问题之一，为了达到稳定的训练我们需要运用一些优化的手段。

环境的稳定性

Agent生活在环境之中，并根据环境的反馈进行学习，但环境是否是稳定的呢？假设agent在学习出门穿衣的技能，它需要学会在冬天多穿，夏天少穿。但是这个agent只会根据当天的反馈来修正自己的行为，也就是说这个agent是没有记忆的。那么这个agent就会在多次失败后终于在冬天学会了多穿衣，但转眼之间到了夏天他又会陷入不断的失败，最终他在夏天学会了少穿衣之后，又会在冬天陷入失败，如此循环不断，永远不会收敛。如果要能够很好的训练，这个agent至少要有一整年的记忆空间，每一批都要从过去的记忆中抽取记忆来进行训练，就可以避免遗忘过去的教训。

在DeepMind的Atari 论文中提到

First, we used a biologically inspired mechanism termed experience replay that randomizes over the data, thereby removing correlations in the observation sequence and smoothing over changes in the data distribution.

意思是，受生物学启发，他们采用了一种叫做经验回放（experience replay）的机制，随机抽取数据来到达“移除观察序列的相关性，平滑数据分布的改变”的目的。

我们已经理解了要有经验回放的记忆，但是为什么一定要随机抽取呢？对此论文认为这个随机抽取可以移除序列相关性、平滑分布中的改变。当如何理解呢？简单的说就是在我们不清楚合理的周期的情况下，能够保证采样的合理性。我们仍然以四季穿衣举例，假设我们不使用随机采样，我们必须在每次训练中都采用365天左右的数据，才能使我们的数据样本分布合理。可是agent并不清楚一年365天这个规律，这恰恰是我们所要学习的内容。采用随机采用，就可以自然的做到数据的分布合理，而且只需要使用记忆中的部分数据，减少单次迭代的计算量。

在这个记忆里，我们并不记录当时的网络参数（分析过程），我们只记录（状态s，动作a，新状态s’, 单步奖励r)。显然，记忆的尺寸不可能无限大。当记忆体增大到一定程度之后，我们采用滚动的方式用最新的记忆替换掉最老的记忆。就像在学习围棋的过程中，有初学者阶段的对局记忆，也有高手阶段的对局记忆，在提升棋艺的角度来看，高手阶段的记忆显然比初学者阶段的记忆更有价值。

说句题外话，其实对于一个民族而言也是一样的。我们这个民族拥有一个非常好的传统，就是记述历史，也就是等于我们这个民族拥有足够大的记忆量，这是我们胜于其他民族的。但是这个历史记录中，掺杂了历史上不同阶段的评价，这些评价是根据当时的经验得出的。而根据DQN的算法描述来看，对我们最有价值的部分其实是原始信息，而不是那些附加在之上的评价，这些评价有正确的部分，也有错误的部分，我们不用去过多关心。我们只需要在今天的认知（也就是最新的训练结果）基础上，对历史原始信息（旧状态、动作、新状态、单步奖励）进行随机的抽样分析即可。

网络稳定性

DQN另一个稳定性问题与目标值计算有关。因为`target = r + gamma * argmax Q(s’)`，所以目标值与网络参数本身是相关，而参数在训练中是不断变化的，所以这会造成训练中的不稳定。一个神经网络可以自动收敛，取决于存在一个稳定的目标，如果目标本身在不断的游移变动，那么想要达到稳定就比较困难。这就像站在平地上的人很容易平衡，但如果让人站在一个不断晃动的木板上，就很难达到平衡。为了解决这个问题，我们需要构建一个稳定的目标函数。

解决的方法是采用两个网络代替一个网络。一个网络用于训练调整参数，称之为策略网络，另一个专门用于计算目标，称之为目标网络。目标网络与策略网络拥有完全一样的网络结构，在训练的过程中目标网络的参数是固定的。执行一小批训练之后，将策略网络最新的参数复制到目标网络中。

经验回放和目标网络的效果见下表（引用自Nature 论文）：

其他DQN优化

关于DQN的优化，这篇文章描述的比较全面 https://zhuanlan.zhihu.com/p/21547911。在之后的实践中考虑是否进一步深入。主要介绍3个改进：

• Double DQN：对目标值计算的优化，a’使用策略网络选择的动作来代替目标网络选择的动作。
• Prioritised replay：使用优先队列（priority queue）来存储经验，避免丢弃早期的重要经验。使用error作为优先级，仿生学技巧，类似于生物对可怕往事的记忆。
• Dueling Network：将Q网络分成两个通道，一个输出V，一个输出A，最后再合起来得到Q。如下图所示（引用自Dueling Network论文）。这个方法主要是idea很简单但是很难想到，然后效果一级棒，因此也成为了ICML的best paper。

我们现在通过一个例子来演练Q-learning算法。在练习强化学习之前，我们需要拥有一个模拟器环境。我们主要的目的是学习编写机器人算法，所以对模拟器环境部分不推荐自己写。直接使用gym来作为我们对实验环境。安装方法：

1

pip install gym

初识环境

我们的实验环境是一个冰湖滑行游戏，你将控制一个agent在冰面到达目标终点，前进方向并不总受你的控制，你还需要躲过冰窟。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import gym
# 构造游戏环境
env = gym.make('FrozenLake-v0')
# 动作空间-> Discrete(4)
print(env.action_space)
# 状态空间-> Discrete(16)
print(env.observation_space)
# 初始化游戏环境，并得到状态s
s = env.reset()
for _ in range(10):
    # 渲染游戏画面
    env.render()
    # 从动作空间中随机选择一个动作a
    a = env.action_space.sample()
    # 执行动作a，得到新状态s，奖励r，是否完成done
    s, r, done, info = env.step(a) # take a random action
    print(s, r, done, info)
# 关闭环境
env.close()

游戏画面示意如下：

1
2
3
4

SFFF       (S: 起点，安全)
FHFH       (F: 冰面，安全)
FFFH       (H: 冰窟，进入则失败)
HFFG       (G: 终点，到达则成功)

Agent结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import random
import math
import gym

class QLAgent():
    q = None
    action_space = None
    epsilon = 0.1 # 探索率
    gamma = 0.99  # 衰减率
    lr = 0.1 # 学习率
    def __init__(self, action_space, state_count, epsilon=0.1, lr=0.1, gamma=0.99):
        self.q = [[0. for a in range(action_space.n)] for s in range(state_count)]
        self.action_space = action_space
        self.epsilon = epsilon
        self.lr = lr
        self.gamma = gamma

    # 根据状态s，选择动作a
    def choose_action(self, s):
        pass

    # 更新状态变化并学习，状态s执行了a动作，得到了奖励r，状态转移到了s_
    def update_transition(self, s, a, r, s_):
        pass

这是一个Agent的一般结构，主要由初始化、选择动作、更新状态变化，三个方法构成。后续的其他算法将依然采用该结构。q表数据使用一个二维数组表示，其大小为 state_count action_count，对于这个项目而言是一个 `16*4` 的大小。

添加Q-table的辅助方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 返回状态s的最佳动作a、及其r值。
def argmax(self, s):
    max_r = -math.inf
    max_a = None
    for a in range(self.action_space.n):
        r = self.q_get(s, a)
        if r > max_r:
            max_a = a
            max_r = r
    return max_a, max_r
# 获得 状态s，动作a 对应的r值
def q_get(self, s, a):
    return self.q[s][a]
# 更新 状态s 动作a 对应的r值
def q_put(self, s, a, v):
    self.q[s][a] = v

Q-learning的关键步骤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def choose_action(self, s):
    if random.random() < self.epsilon:
        # 按一定概率进行随机探索
        return self.action_space.sample()
    # 返回最佳动作
    a, _ = self.argmax(s)
    return a

def update_transition(self, s, a, r, s_):
    q = self.q_get(s, a)
    _, r_ = self.argmax(s_)
    # Q <- Q + a(Q' - Q)
    # <=> Q <- (1-a)Q + a(Q')
    q = (1-self.lr) * q + self.lr * (r + self.gamma * r_)
    self.q_put(s, a, q)

训练主循环

我们进行10000局游戏的训练，每局游戏执行直到完成。

1
2
3
4
5
6
7
8
9
10
11
12
13

env = gym.make('FrozenLake-v0')
agent = QLAgent(env.action_space, env.observation_space.n)
for epoch in range(10000):
    s = env.reset()
    done = False
    while not done:
        # env.render()  # 训练过程不需要渲染
        a = agent.choose_action(s) # 选择动作
        s_, r, done, info = env.step(a) # 执行动作
        agent.update_transition(s, a, r, s_) # 更新状态变化
        s = s_
# 显示训练后的Q表
print(agent.q)

测试效果

在测试中，我们只选择最佳策略，不再探索，也不再更新Q表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 获胜次数
total_win = 0
for i in range(10000):
    s = env.reset()
    done = False
    while not done:
        # 选择最佳策略
        a, _ = agent.argmax(s)
        # 执行动作 a
        s_, r, done, info = env.step(a)
        if done and r == 1:
            total_win += 1
        s = s_
print('Total win=', total_win)
env.close()

最终测试的效果是在1万局中获胜了7284次，说明达到了不错的实验效果。

完成图像分类之类的监督学习任务，已经没有特别大的难度。我们希望AI能够帮助我们处理一些更加复杂的任务，比如：下棋、玩游戏、自动驾驶、行走等。这一类的学习任务被称为强化学习。

K摇臂赌博机

我们可以考虑一个最简单的环境：一个动作可立刻获得奖励，目标是使每一个动作的奖励最大化。对这种单步强化学习任务，可以设计一个理论模型——“K-摇臂赌博机”。这个赌博机有K个摇臂，赌徒在投入一个硬币后可一选择按下一个摇臂，每个摇臂以一定概率吐出硬币，但这个概率赌徒并不知道。赌徒的目标是通过一定的策略最大化自己的奖赏，即获得最多的硬币。最终所获得的总奖励被称为累计奖励。

对于这个简单模型，若要知道每个摇臂的概率，我们只需要进行足够多的尝试即可，这是“仅探索”策略；若要奖励最大化，则需要执行奖赏概率最大的动作即可，这是“仅利用”策略。但在更复杂的环境中，我们不可能对每一个状态的每个动作都进行足够多的探索。比如围棋，我们后续的探索是需要依赖于之前的探索的。因此我们需要在探索和利用之间进行平衡。我们在学习的过程中，必须要保持一定的概率`epsilon`进行探索，其余时候则执行学习到的策略。

基本概念术语

为了便于分析讨论，我们定义一些术语。

• 机器agent处于环境`E`中。

• 状态空间为`S`，每个状态`s in S`是机器感知到的环境描述。

• 机器能够采取的可采取的动作a的集合即动作空间`A`，`a in A`。

• 转移函数`P`表示：当机器执行了一个动作`a`后，环境有一定概率从状态`s`改变为新的状态`s’`。即：`s’=P(s, a)`

• 奖赏函数`R`则表示了执行动作可能获得的奖赏`r`。即：`r=R(s,a)`。

• 环境可以描述为`E=<<S, A, P, R>>`。

• 强化学习的任务是习得一个策略（policy）`pi`，使机器在状态`s`下选择到最佳的`a`。策略有两种描述方法：

  1. `a=pi(s)` 表示状态`s`下将执行动作`a`，是一种确定性的表示法。
  2. `pi(s, a)` 表示状态`s`下执行动作`a`的概率。这里有 `sum_a pi(s,a)=1`

• 累计奖励指连续的执行一串动作之后的奖励总和。

• `Q^(pi)(s, a)`表示在状态`s`下，执行动作`a`，再策略`pi`的累计奖励。为方便讨论后续直接写为`Q(s,a)`。

• `V^(pi)(s)` 表示在状态`s`下，使用策略`pi`的累计奖励。为方便讨论后续直接写为`V(s)`。

强化学习往往不会立刻得到奖励，而是在很多步之后才能得到一个诸如成功/失败的奖励，这是我们的算法需要反思之前所有的动作来学习。所以强化学习可以视作一种延迟标记的监督学习。

Q-learning

对于我们要学习的`Q(s,a)`函数，我们可以使用一个Q-table来表示。Q-table是一个二维表，记录每个状态`s in S, a in A`的`Q`值。Q表被初始化为0的状态。在状态`s`执行了动作`a`之后，得到状态`s’`，奖励`r`。我们将潜在的`Q`函数记为`Q_(real)`，其值为当前奖励r与后续状态`s’`的最佳累计奖励之和。则有：

` Q_(real)(s, a) = r + gamma * argmax_aQ(s’, a) `
` err = Q_(real)(s, a) - Q(s, a) `

其中`gamma`为`Q`函数的偏差，`err`为误差，`alpha`为学习率。 可得出更新公式为：

` Q(s, a) leftarrow Q(s, a) + alpha*err `
即：
` Q(s,a) leftarrow (1-alpha)Q(s,a) + alpha(r + gamma * argmax_aQ(s’, a)) `

以上公式即为Q-learning的关键

算法描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 初始化Q表
for s in S:
  for a in A:
    Q(s, a) = 0
# 训练过程
for i in range(N):
  if rand() < epsilon:
    a = 从 A 中随机选取一个动作
  else:
    a = 从 A 中选取使 Q(a) 最大的a
  # 从环境中获得反馈
  r = R(s, a)
  s1 = P(s, a)
  # 更新Q表
  Q(s,a) = (1-alpha)*Q(s,a) + alpha * (r + gamma * argmax Q(s1, a) - Q(s, a))
  s = s1

下图是一个Q表内存结构，在经过一定的学习后，Q表的内容将能够不断逼近每个状态的每个动作的累计收益。

深度神经网络输出的结果与标注结果进行对比，计算出损失，根据损失进行优化。那么输出结果、损失函数、优化方法就需要进行正确的选择。

常用损失函数

pytorch 损失函数的基本用法

1
2

criterion = LossCriterion(参数)
loss = criterion(x, y)

Mean Absolute Error
torch.nn.L1Loss
Measures the mean absolute error.

Mean Absolute Error/ L1Loss

nn.L1Loss

很少使用

Mean Square Error Loss

nn.MSELoss

针对数值不大的回归问题。

Smooth L1 Loss

nn.SmoothL1Loss

它在绝对差值大于1时不求平方，可以避免梯度爆炸。大部分回归问题都可以适用，尤其是数值比较大的时候。

Negative Log-Likelihood Loss

torch.nn.NLLLoss，一般与 LogSoftmax 成对使用。使用时 loss(softmaxTarget, target)。用于处理多分类问题。

1
2
3
4
5
6
7
8

m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss()
# input is of size N x C = 3 x 5， C为分类数
input = torch.randn(3, 5, requires_grad=True)
# each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 4])
output = loss(m(input), target)
output.backward()

Cross Entropy Loss

nn.CrossEntropyLoss 将 LogSoftmax 和 NLLLoss 绑定到了一起。所以无需再对结果使用Softmax

1
2
3
4
5

loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()

BCELoss

二分类问题的CrossEntropyLoss。输入、目标结构是一样的。

1
2
3
4
5
6

m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(m(input), target)
output.backward()

Margin Ranking Loss

常用户增强学习、对抗生成网络、排序任务。给定输入x1，x2，y的值是1或-1，如果y==1表示x1应该比x2的排名更高，y==-1则相反。如果y值与x1、x2顺序一致，那么loss为0，否则错误为 y*(x1-x2)

Hinge Embedding Loss

y的值是1或-1，用于衡量两个输入是否相似或不相似。

Cosine Embedding Loss

给定两个输入x1，x2，y的值是1或-1，用于衡量x1和x2是否相似。

其中cos(x1, x2)表示相似度

各种优化器

大多数情况Adam能够取得比较好的效果。SGD 是最普通的优化器, 也可以说没有加速效果, 而 Momentum 是 SGD 的改良版, 它加入了动量原则. 后面的 RMSprop 又是 Momentum 的升级版. 而 Adam 又是 RMSprop 的升级版. 不过从这个结果中我们看到, Adam 的效果似乎比 RMSprop 要差一点. 所以说并不是越先进的优化器, 结果越佳.

1
2
3
4
5
6
7
8

# SGD 就是随机梯度下降
opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
# momentum 动量加速,在SGD函数里指定momentum的值即可
opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
# RMSprop 指定参数alpha
opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
# Adam 参数betas=(0.9, 0.99)
opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))

本文假设读者已经了解了CNN的基本原理。在实际的项目中，会发现CNN有多个参数需要调整，本文主要目的在于理清各个参数的作用。

卷积核 kernel

Kernel，卷积核，有时也称为filter。在迭代过程中，学习的结果就保存在kernel里面。深度学习，学习的就是一个权重。kernel的尺寸越小，计算量越小，一般选择3x3，更小就没有意义了。

结果是对卷积核与一小块输入数据的点积。

层数 Channels

所有位置的点积构成一个激活层。

如果我们有6个卷积核，我们就会有6个激活层。

步长 Stride

上图是每次向右移动一格，一行结束向下移动一行，所以stride是1x1，如果是移动2格2行则是2x2。

填充 Padding

Padding的作用是为了获取图片上下左右边缘的特征。

池化 Pooling

卷积层为了提取特征，但是卷积层提取完特征后特征图层依然很大。为了减少计算量，我们可以用padding的方式来减小特征图层。Pooling的方法有MaxPooling核AveragePooling。

推荐看一下李飞飞的这篇slide

PyTorch 中的相关方法

• torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode=’zeros’)

• torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)

  • stride 默认与kernel_size相等

• torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)

• Tensor.view(*shape) -> Tensor

  • 用于将卷积层展开为全连接层

    1 2 3 4 5 6 7 8 9

    >>> x = torch.randn(4, 4) >>> x.size() torch.Size([4, 4]) >>> y = x.view(16) >>> y.size() torch.Size([16]) >>> z = x.view(-1, 8) # the size -1 is inferred from other dimensions >>> z.size() torch.Size([2, 8])

MNIST例子

MNIST 数据集的输入是 1x28x28 的数据集。在实际开发中必须要清楚每一次的输出结构。

• 我们第一层使用 5x5的卷积核，步长为1，padding为0，28-5+1 = 24，那么输出就是 24x24。计算方法是 (input_size - kernel_size)/ stride + 1。
• 我们第二层使用 2x2的MaxPool，那么输出为 12x12.
• 第三层再使用5x5，卷积核，输出则为 12-5+1，即 8x8。
• 再使用 2x2 MaxPool，输出则为 4x4。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    """ConvNet -> Max_Pool -> RELU -> ConvNet -> Max_Pool -> RELU -> FC -> RELU -> FC -> SOFTMAX"""
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, 5, 1)
        self.conv2 = nn.Conv2d(10, 20, 5, 1)
        self.fc1 = nn.Linear(4*4*20, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.max_pool2d(x, 2, 2)
        x = F.relu(self.conv2(x))
        x = F.max_pool2d(x, 2, 2)
        x = x.view(-1, 4*4*20)
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

以上代码摘自 https://github.com/floydhub/mnist

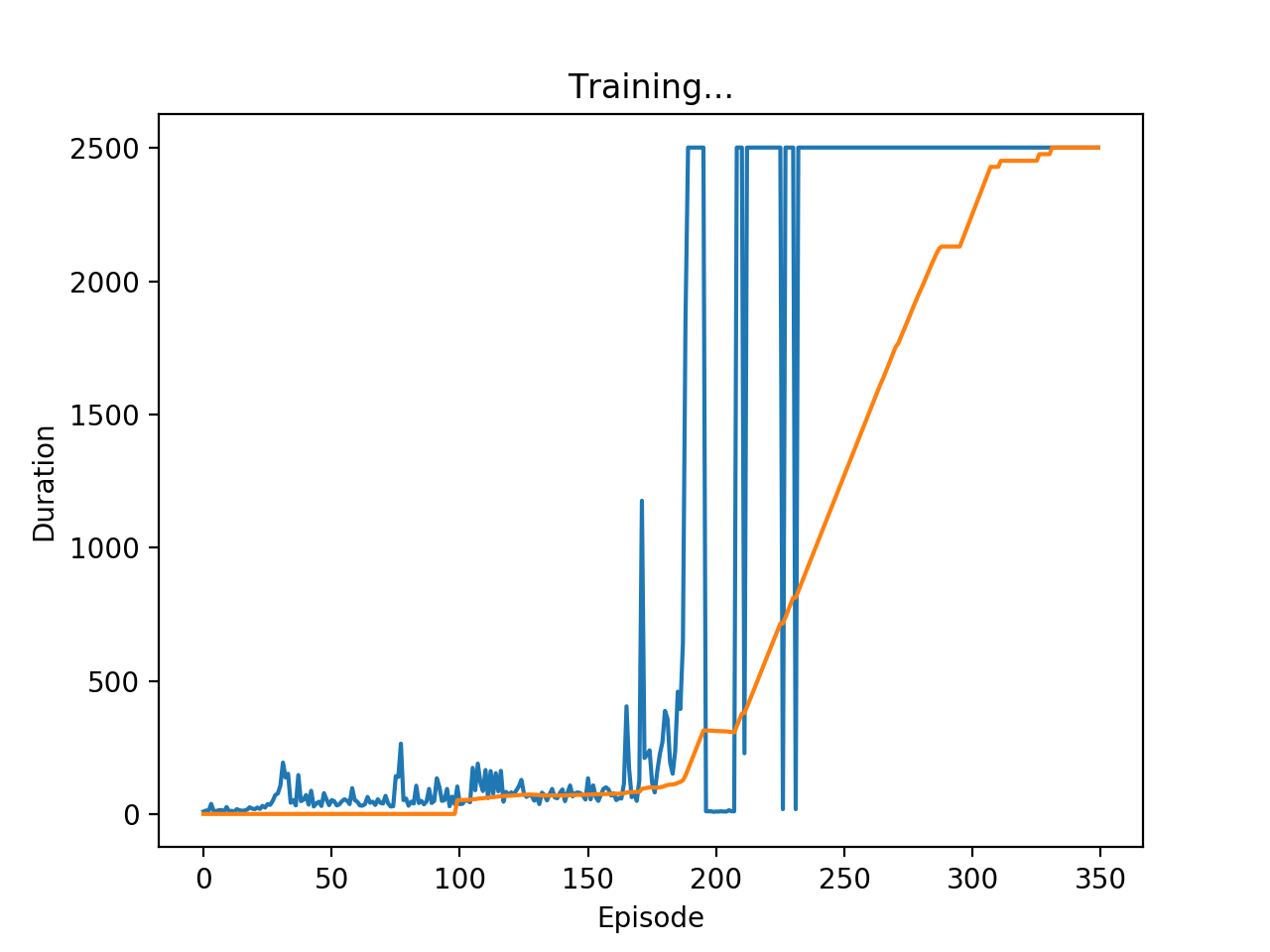
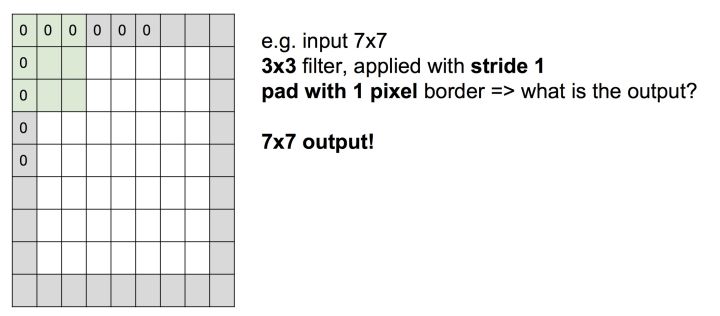
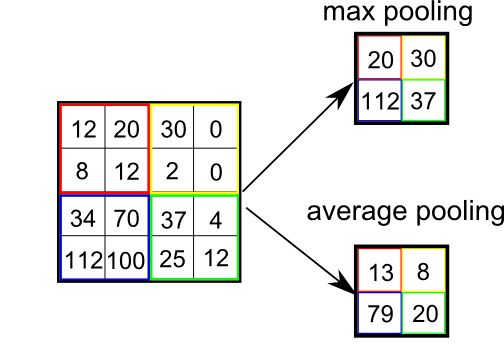
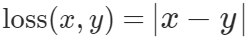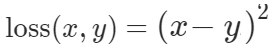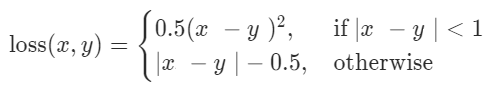本文写于2017年12月，获Udacity专栏转载。今将其搬运至我的博客。

2016年3月，Alpha Go Master击败最强的人类围棋选手之一李世石。击败李的版本，在训练过程中使用了大量人类棋手的棋谱。2017年10月19日，DeepMind公司在《自然》杂志发布了一篇新的论文，AlphaGo Zero——它完全不依赖人类棋手的经验，经过3天的训练，Alpha Go Zero击败了Master版本。AlphaGo Zero最重要的价值在于，它不仅仅可以解决围棋问题，它可以在不需要知识预设的情况下，解决一切棋类问题，经过几个小时的训练，已击败最强国际象棋冠军程序Stockfish。其应用场景非常广泛。

AlphaGo Zero 采用了蒙特卡洛树搜索＋深度学习算法，本文将尽可能用简单易懂的语言解释其工作原理。

树搜索

从一个棋盘的初始状态，开始思考下一步如何走。我们可以回顾一下我们思考的过程，我们会思考自己可以有哪几种走法，如果我走了这里，对手可能会走哪里，那么我还可以在哪里走。我和对手都会选择最有利的走法，最终价值最大的那一手，就是我要选择的下法。很明显这个思维过程是一颗树，为了寻找最佳的行棋点的过程，就是树搜索。

围棋第一手有361种下法，第二手有360种，第三手有359，依次类推，即一共有 361! 种下法，考虑到存在大量不合规则的棋子分布，合理的棋局约占这个数字的1.2%(Counting Legal Positions in Go). 约为2.081681994 * 10^170。这个一个天文数字，比目前可观测宇宙的所有原子数还要多。要进行完全树搜索，是不可能的。因此我们必须进行剪枝，并限制思考的深度。所谓剪枝，就是指没必要考虑每种下法，我们只需考虑最有价值的几手下法。所谓限制思考的深度，就是我们最多只思考5步，10步，20步。常见的算法是Alpha-beta剪枝算法。但是，剪枝算法也有它的缺陷，它很有可能过早的剪掉了后期价值很大走法。

蒙特卡洛方法

简而言之，蒙特卡洛方法(Monte Carlo method)，是一种“统计模拟方法”。20世纪40年代，为建造核武器，冯.诺伊曼 等人发明了该算法。因赌城蒙特卡洛而得名，暗示其以概率作为算法的基础。

假设我们要计算一个不规则形状的面积，我们只需在包含这个不规则形状的矩形内，随机的掷出一个点，每掷出一个点，则N+1，如果这个点在不规则图形内则W+1。落入不规则图形的概率即为 W/N。当掷出足够多的点之后，我们可以认为：不规则图形面积＝矩形面积＊W/N。

要应用蒙特卡洛算法的问题，首先要将问题转化为概率问题，然后通过统计方法将其问题的解估计出来。

蒙特卡洛树搜索（MCTS）

1987年Bruce Abramson在他的博士论文中提出了基于蒙特卡洛方法的树搜索这一想法。这种算法简而言之是用蒙特卡洛方法估算每一种走法的胜率。如果描述的再具体一些，通过不断的模拟每一种走法，直至终局，该走法的模拟总次数N，与胜局次数W，即可推算出该走法的胜率为 W/N。

该算法的每个循环包含4个步骤：选择、扩展、仿真、反向传播。一图胜千言。

图中N表示总模拟次数，W表示胜局次数。每次都选择胜率最大的节点进行模拟。但是这样会导致新节点无法被探索到。为了在最大胜率和新节点探索上保持平衡，UCT（Upper Confidence Bound，上限置信区间算法）被引入。所谓置信区间，就是概率计算结果的可信度。打个比方，如果掷了3次硬币，都是正面朝上，我们就认为掷硬币正面朝上概率是100%，那肯定是错误的，因为我们的样本太少了。所以UCT就是用来修正这个样本太少的问题。具体公式如下：

其中wi 是i节点的胜利次数，ni是i节点的模拟次数，Ni是所有模拟次数，c是探索常数，理论值为 √2，可根据经验调整。公式的后半部分，探索次数越少，值会越大，所以，那些被探索比较少的点，会获得更多的探索机会。

蒙特卡洛树搜索算法因为是直接模拟到游戏终局，所以这种算法更加的准确，而且并不需要一个明确的“估值函数”，你只需要实现游戏机制就足够了。而且，蒙特卡洛算法，可以随时终止，根据其训练的时间给予近似的最优结果。

但是对于围棋这种游戏而言，它的选择点依然太多，这棵树会非常的大。可能有一个分支早已被丢弃，那么它将不会被统计，这可能是李世石能够在第四局击败AlphaGo的主要原因。对于这类情况，我们依然需要依赖一个好的估值函数来辅助。

深度学习

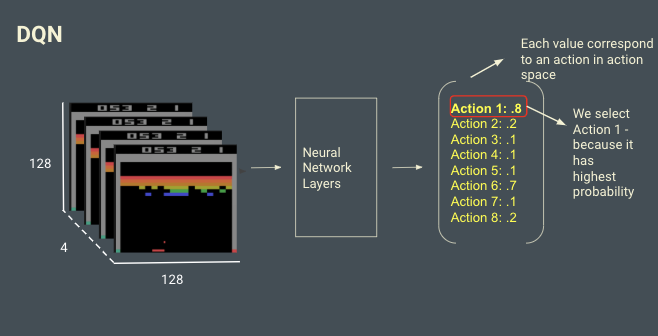
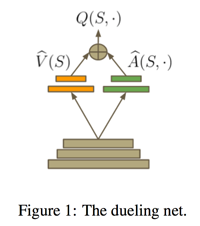
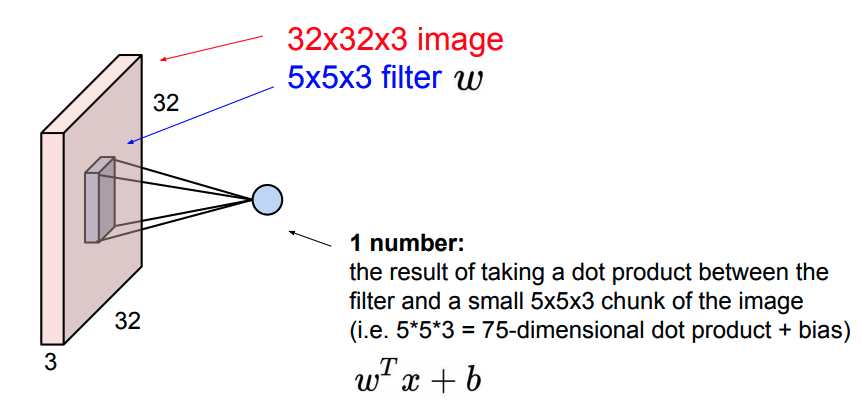
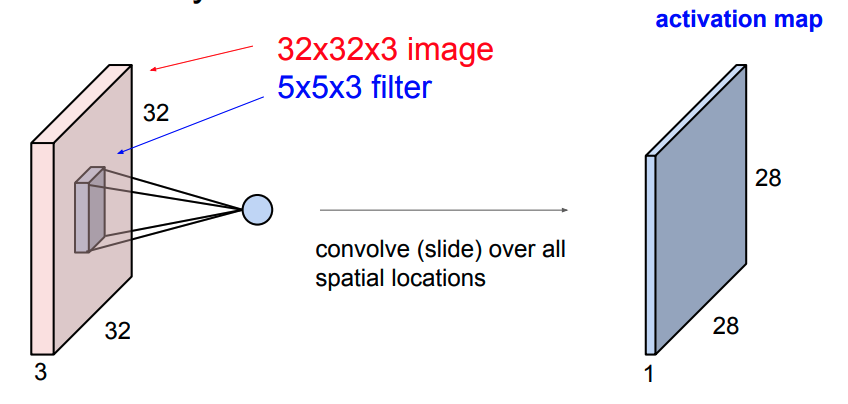
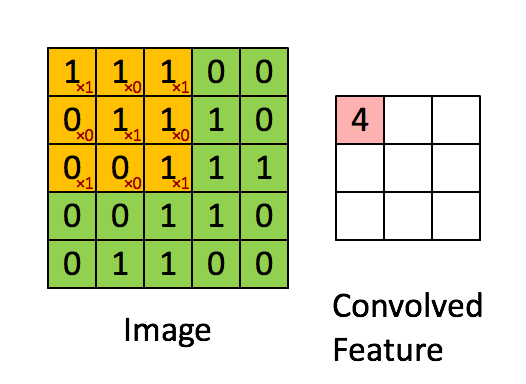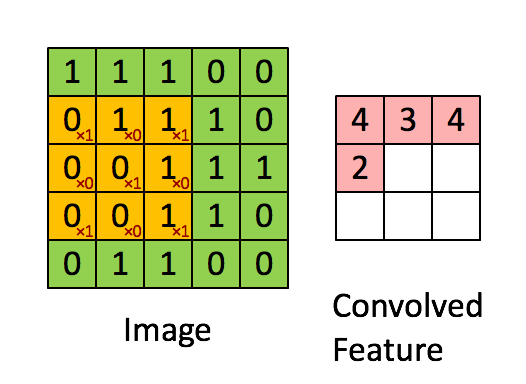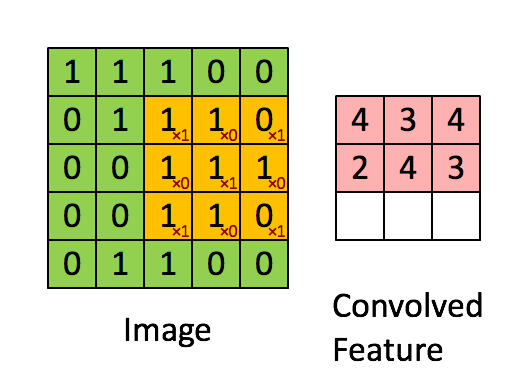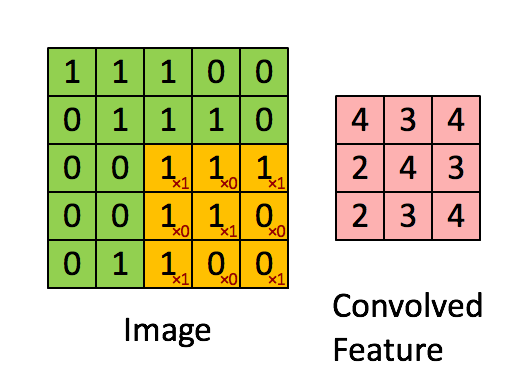
近年来，深度卷积神经网络在视觉领域取得很大的成功，如图片分类，人脸识别等。深度学习的网络结构在此不赘述，简而言之，深度学习是一个最优化算法。

我们可以将深度神经网络理解为一个黑盒，这个黑盒接收一批输入，得到一个输出，并根据输出计算出损失（误差），这个误差会反馈给黑盒，当给了足够多的数据之后，这个黑盒将具备一个特性，就是使误差最小化。

如果这么说还是难以理解的话，可以打个比方：深度神经网络是一种生物，它喜欢吃糖，有学习的能力，你给它看一张图片，它告诉你是猫还是狗，如果它猜对了，你就给它一颗糖，猜错了，就不给糖，久而久之，它就有了分辨猫狗的能力。作为创造者，你甚至不知道它是如何分辨猫狗的，但是它做到了，看得越多，识别的就越准。

这里至关重要的是——输入是什么？输出是什么？什么时候给糖的动作，也就是损失函数如何设计？在实际的操作过程中，网络结构的设计也很重要，这里不再细述。

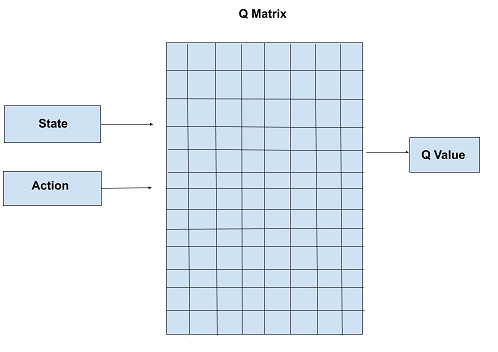
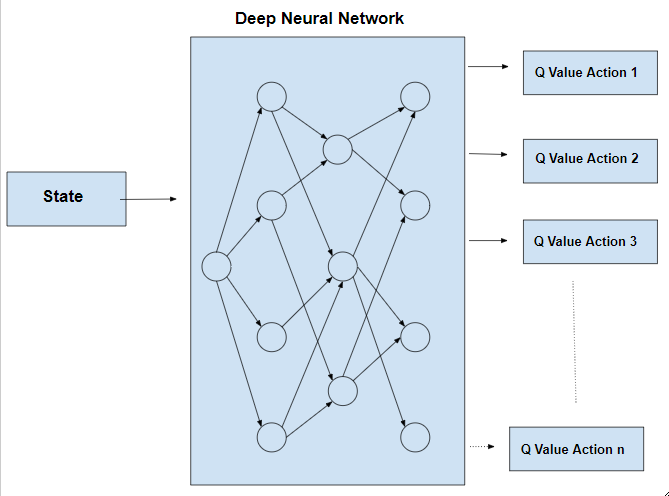
对于围棋来说，深度网络可以用来评估下一步的主要选点（降低树的宽度），以及评估当前局面的值。

AlphaGo Zero

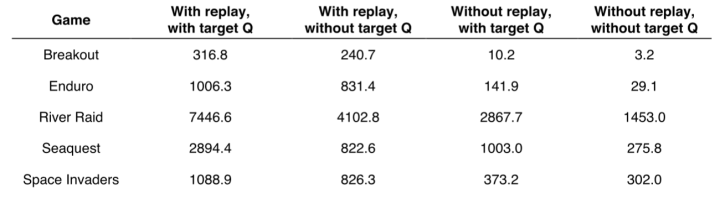
在AlphaGo Lee版本，有两个神经网络，一个是策略网络，是一个有监督学习，它利用了大量的人类高手的对弈棋局来评估下一步的可能性，另一个是价值网络，用来评价当前局面的评分。而在AlphaGo Zero版本，除了围棋规则外，没有任何背景知识，并且只使用一个神经网络。

这个神经网络以19x19棋盘为输入，以下一步各下法的概率以及胜率为输出，这个网络有多个batch normalization卷积层以及全连接层。

AlphaGo Zero的核心思想是：MCTS算法生成的对弈可以作为神经网络的训练数据。 还记得我们前面说过的深度学习最重要的部分吗？输入、输出、损失！随着MCTS的不断执行，下法概率及胜率会趋于稳定，而深度神经网络的输出也是下法概率和胜率，而两者之差即为损失。随着训练的不断进行，网络对于胜率的下法概率的估算将越来越准确。这意味着什么呢？这意味着，即便某个下法AGZ没有模拟过，但是通过神经网络依然可以达到蒙特卡洛的模拟效果！也就是说，我虽然没下过这手棋，但凭借我在神经网络中训练出的“棋感”，我可以估算出这么走的胜率是多少！

AlphaGo Zero的对弈过程只需应用深度网络计算出的下法概率、胜率、MCTS的置信区间等数据即可进行选点。

AlphaGo Zero 论文节选

a:自我对弈过程s1，…，sT。 在每个状态st, 使用最近一次的网络fθ，执行一次MCTS αθ （见图2）。 下法根据MCTS计算的搜索概率而选择，at ~ πt. 评价终止状态sT，根据游戏规则来计算胜利者z。
b: AlphaGo Zero的神经网络训练。网络使用原始的棋盘状态st作为输入，通过数个卷积层，使用参数θ，输出有向量 pt, 表示下法的分布概率，以及一个标量vt，表示当前玩家在st的胜率。网络参数θ将自动更新，以最大化策略向量pt和搜索概率πt的相似性，并最小化预测赢家vt与实际赢家z的误差。新参数将应用于下一次自我对弈a的迭代。

a: 每次模拟选择的分支，有最大Q+U, 其中Q是动作价值，U是上限置信，U依赖于一个存储在分支上的优先概率P和该分支的访问次数N（每访问一次N+1）。
b: 扩展叶节点，神经网络（P(s, .), V(s)) = fθ(s)评估s; 将向量P的值被存储在s的扩展边上。
c: 根据V更新动作价值（action-value)Q，反映所有该动作的子树的平均值。
d: 一旦搜索结束，搜索概率π被返回，与 Ν^(1/τ) 成正比，N是每个分支的访问次数，而τ是一个参数控制着温度（temperature）。

AlphaGo Zero的应用

AGZ算法本质上是一个最优化搜索算法，对于所有开放信息的离散的最优化问题，只要我们可以写出完美的模拟器，就可以应用AGZ算法。所谓开放信息，就像围棋象棋，斗地主不是开放信息，德扑虽然不是开放信息，但本身主要是概率问题，也可以应用。所谓离散问题，下法是一步一步的，变量是一格一格，可以有限枚举的，比如围棋361个点是可以枚举的，而股票、无人驾驶、星际争霸，则不是这类问题。Deepmind要攻克的下一个目标是星际争霸，因为它是不完全信息，连续性操作，没有完美模拟器（随机性），目前在这方面AI还是被人类完虐

所以看到AG打败人类，AGZ打败AG，就认为人工智能要打败人类了，这种观点在未来可能成立，但目前还有点危言耸听。距离真正打败人类，AGZ还差得很远。