双向反射分布函数(bidirectional reflectance distribution function)$f_r(omega_i,omega_r)$是一个计算光照反射量的函数。$omega_i$表示输入光角度,$omega_r$表示反射光角度,函数返回反射光辐射率。$omega$由球面坐标系的$phi$,$theta$角度表示,因此brdf函数共有4个参数。brdf的单位是每立体角$sr^(-1)$。
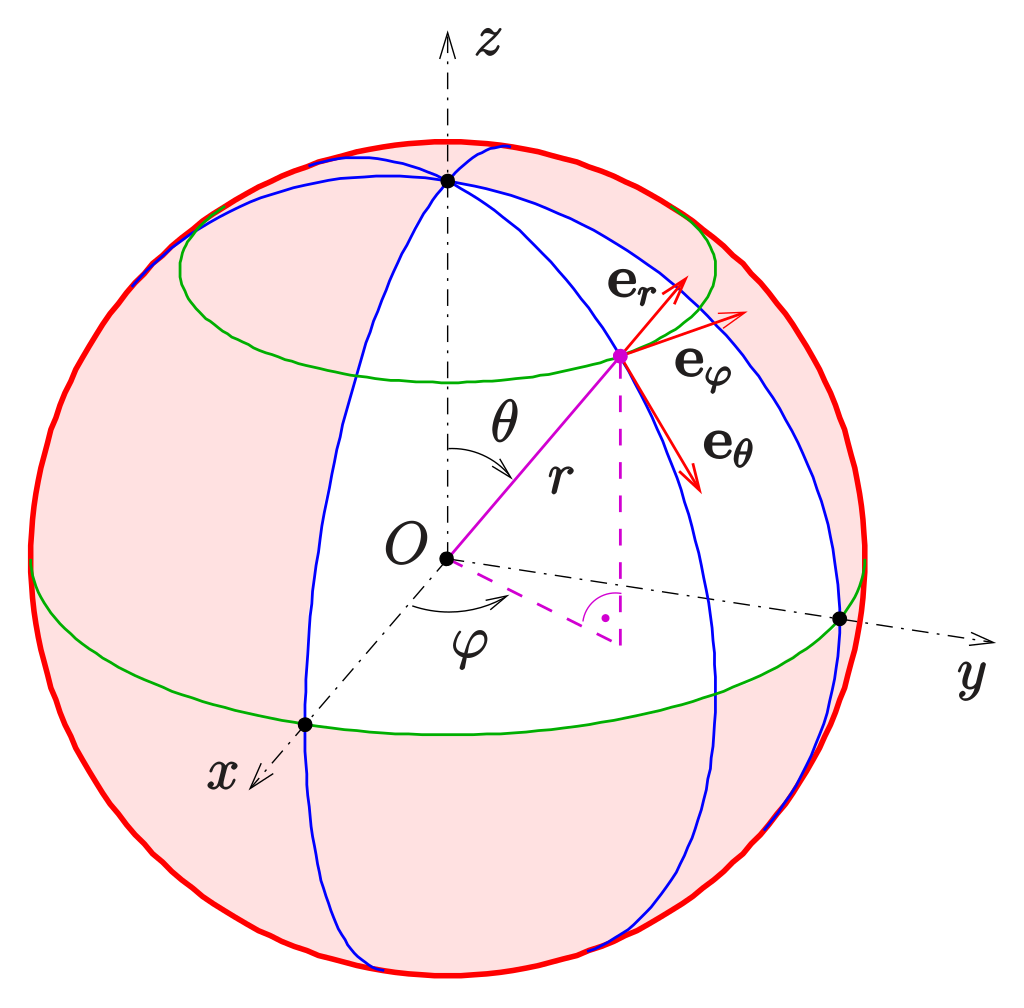
辐射度量学(Radiometry)
| 物理量 | 符号 | 公式 | 国际单位制 | 单位符号 | 注释 |
|---|---|---|---|---|---|
| 辐射能(Radiant energy) | $Q_e$ | 焦耳 | $J$ | 能量。 | |
| 辐射通量(Radiant flux) | $Phi_e$ | $Phi=(dQ)/(dt)$ | 瓦特 | $W$ | 每单位时间的辐射能量,亦作“辐射功率”。 |
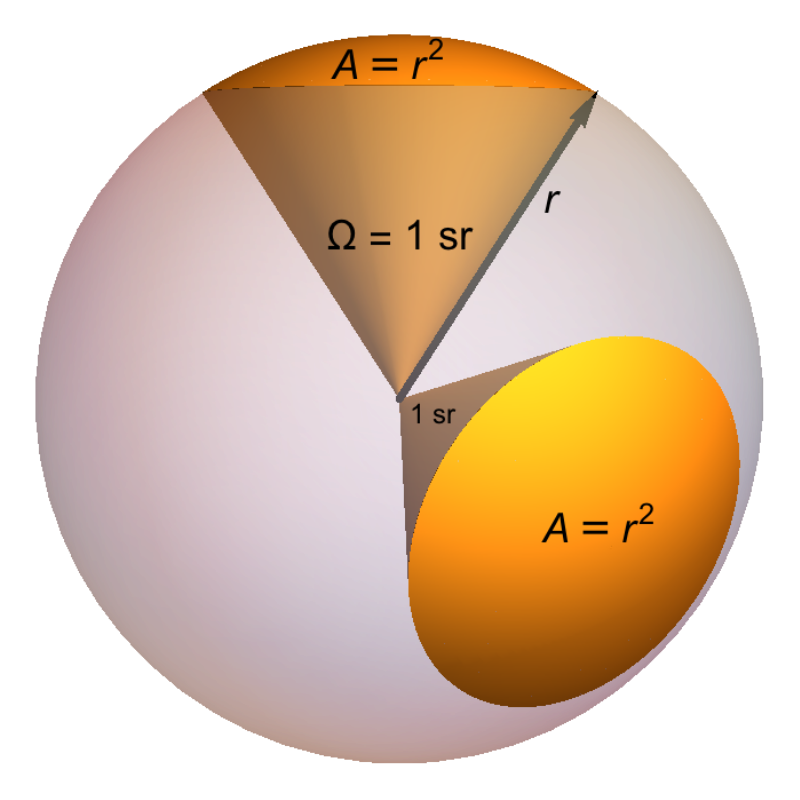
| 辐射强度(Radiant intensity) | $I_e$ | $I=(dPhi)/(d omega) | 瓦特每球面度 | $W*sr^(-1)$ | 每单位立体角的辐射通量。 |
| 辐照度(Irradiance)(辉度) | $E_e$ | $E=(dPhi)/(dA)=int_(Omega) L(omega)cos theta d omega$ | 瓦特每平方米 | $W*m^(-2)$ | 入射表面的辐射通量 |
| 辐射率(Radiance)(光亮度) | $L_e$ | $(d^2Phi)/(dAcos theta d omega)$ | 瓦特每球面度每平方米 | $W*sr^(-1)*m^(-2)$ | 每单位立体角每单位投射表面的辐射通量。相当于辐射强度在dA上的微分 |
BRDF由Fred Nicodemus在1965年提出,函数如下:
$$f_r(omega_i,omega_r) = (dL_r(omega_r))/(dE_i(omega_i)) = (dL_r(omega_r))/(L_i(omega_i)cos theta_i d omega_i) $$

这个公式之所以定义为辐射率(radiance)和辐照度(irradiance)之比,而不是radiance和radiance之比,或irradiance和irradiance之比。是因为当考虑入射时,我们需要考虑入射光在面积上的分量,所以irradiance译为辐照度。当考虑反射时,我们需要考虑每立体角的辐射通量,并且这个辐射通量最终投影在屏幕(视网膜)面积上的辐射通量,因此我们用辐射率。如果我们用点光源,入射光的计算似乎也是可以用辐射率的,但有时我们还要考虑平行光的情况,那么对于入射光就不存在每立体角的概念了,因此对于入射光照我们用辐照度,反射我们用辐射率。
基于物理的BRDF模型(PBR,Physically-based rendering)
次表面散射(Subsurface scattering)
是一些半透明物质比如皮肤、玉石、大理石、塑料等。当光入射到材料表面后,一部分被反射、一部分被吸收、还有一部分经历透射,透射光在材料内部进行多次不规则的反射之后,又从不同角度反射了回来。
菲涅尔反射(Fresnel Reflectance)
当光从一种折射率为$n_1$的介质向另一种折射率为$n_2$的介质传播时,在两者的交界处可能会同时发生光的反射和折射。菲涅尔方程描述了光波的不同分量被折射和反射的情况,也描述了波反射时的相变。光线会随着我们的观察角度而反射不同的亮度,当我们以垂直与水面的角度观察池塘时,我们可以看到池塘的底部,但当我们以平行于水面的角度观察水面时,反射光则会很强我们无法看到池底。
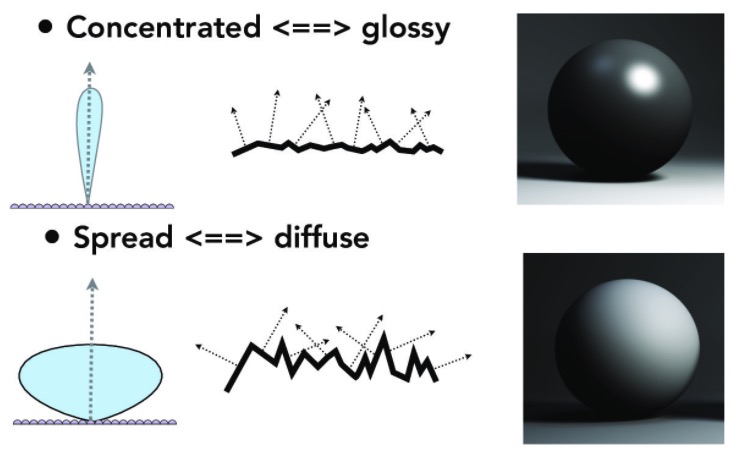
微表面理论(Microfacet Theory)
微表面理论假设材质的表面是由不同方向的微小细节平面(microfacet)所构成,反射光线由这些微表面的法线分布决定。我们用法线分布函数(Normal Distribution Function,NDF),D(h) 来描述表面的法线分布概率。h表示视角与入射光角度之间的半程向量。
$$f(i,o) = (F(i,h)G(i,o,h)D(h))/(4(n,i)(n,o))$$
其中F(i,h)表示菲涅尔项,表示所有反射的比例。G(i,o,h) 表示自投影项,当光线几乎平射于微表面时,光线则将被粗糙的表面自我遮挡掉。D(h)表示法线分布。
参考:
Wikipedia:《Bidirectional reflectance distribution function》
《Real-Time Rendering, 4th edition》