1.勾股定理——宇宙的密码
$a^2+b^2=c^2$。下图是勾股定理的一个直观证明。
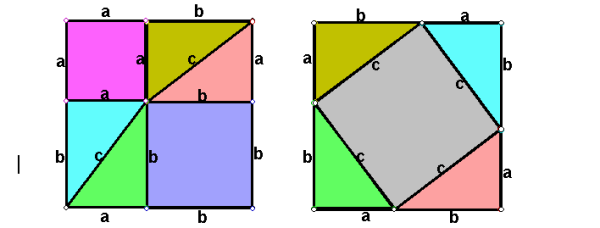
2. 余弦定理,角与边的关系
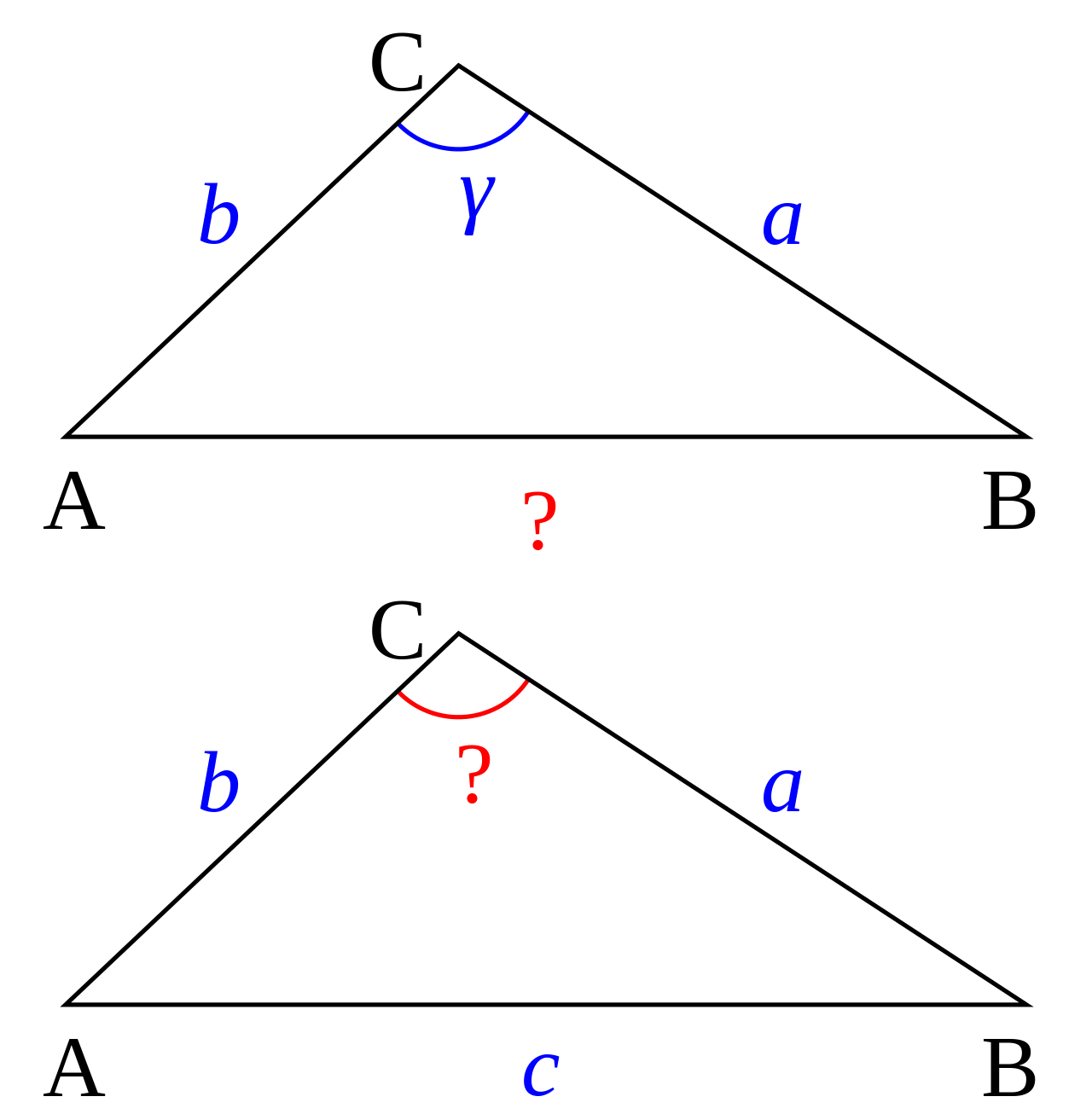
三条边可以确定一个三角形,已知三角形的三条边长,如何求出其角度呢?
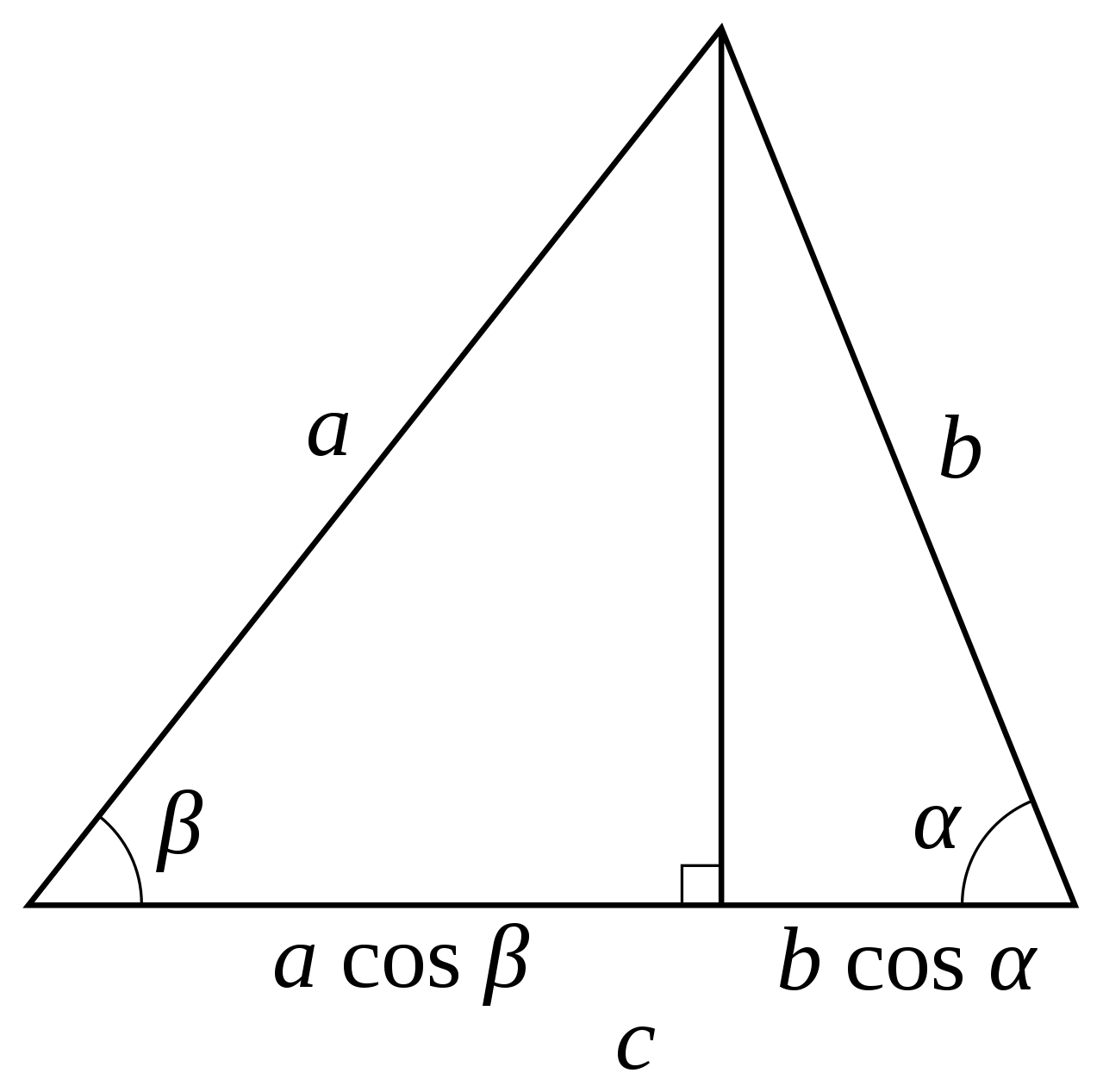
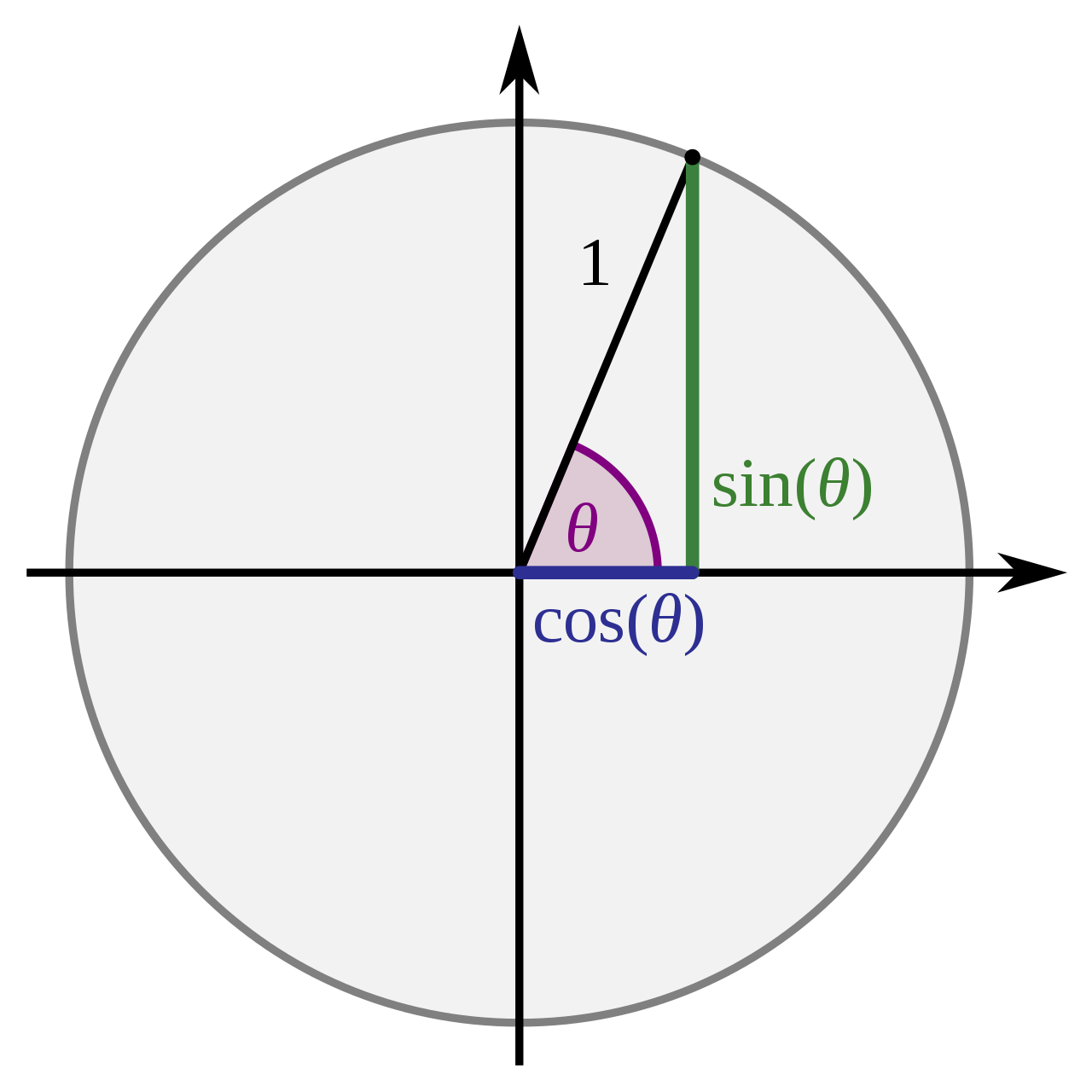
由$cos,sin$定义可知
$$ c = a * cos beta + b * cos alpha $$
两边同乘c得:
$$ c^2 = ac * cos beta + bc * cos alpha $$
同理可得:
$$ a^2 = ac cos beta + ab * cos gamma $$
$$ b^2 = bc cos alpha + ab cos gamma $$
故:$$ a^2+b^2-c^2 = 2abcosgamma $$
可得:$$ c^2 = a^2 + b^2 - 2ab cos gamma $$
3. 向量的定义(方向)
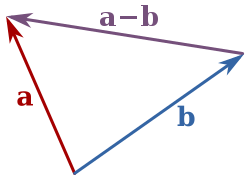
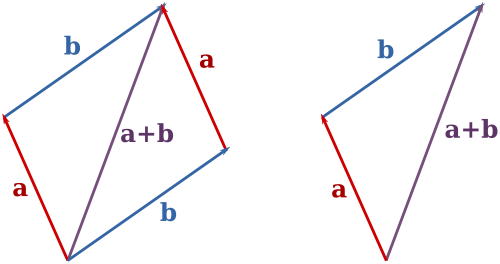
$$令 vec c = vec a - vec b$$, $$theta$$为$$vec a$$ $$vec b$$ 的夹角。余弦定理可以用向量形式写成 $$ | vec c |^2 = |vec a|^2 + |vec b|^2 - 2 |vec a| |vec b| cos theta $$
4. 点积(dot product)的代数定义
两个向量的点积是一个标量。向量$$vec a=[a_1, a_2, … a_n]$$与向量$$vec b=[b_1, b_2, … b_n]$$的点积定义为: $$ vec a * vec b = sum_(i=1)^n a_i b_i = a_1 b_1 + a_2 b_2 + … a_n b_n $$。
点积有以下性质(证略):
- 满足交换律 $$vec a * vec b = vec b * vec a$$
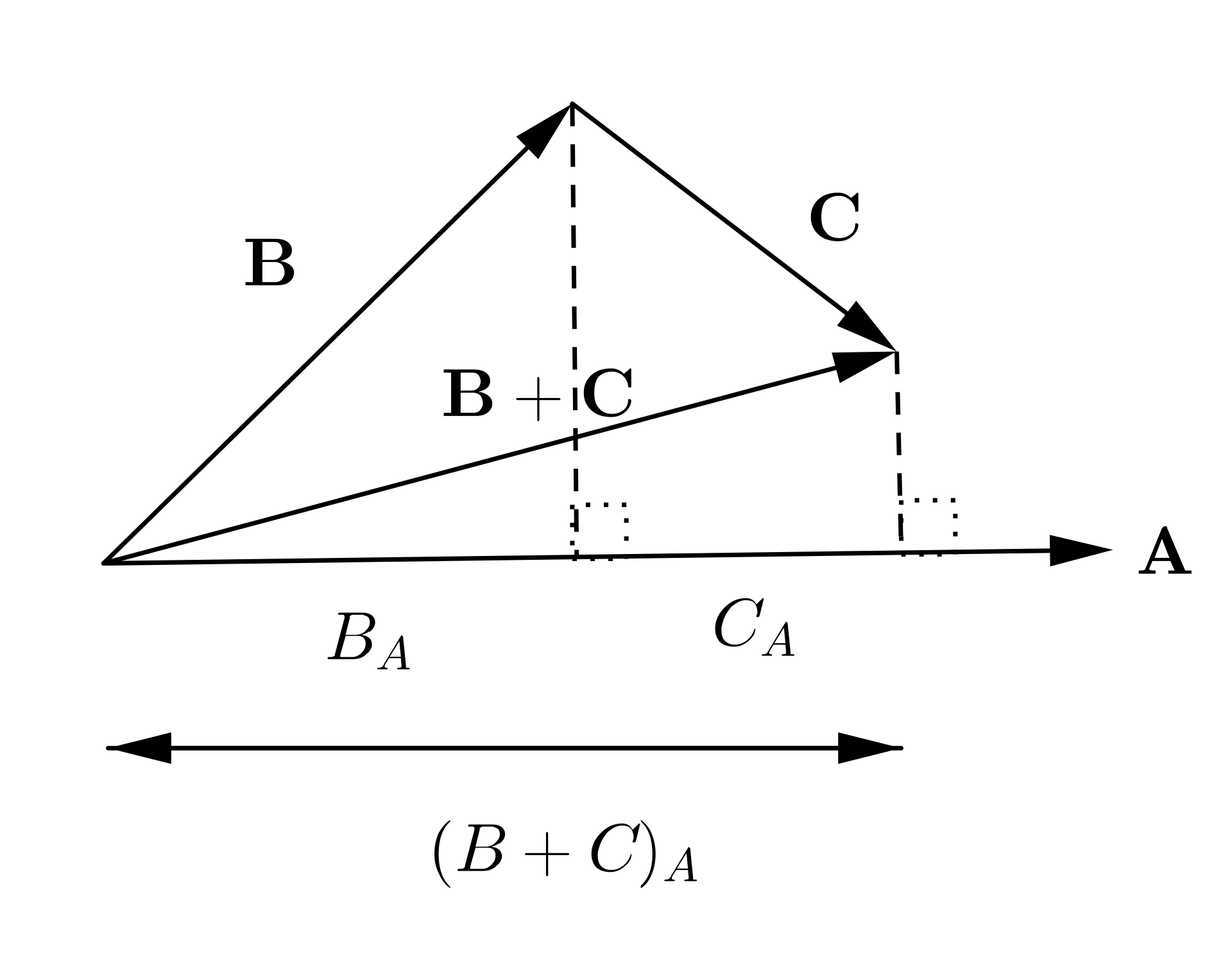
- 满足分配律 $$vec a * (vec b + vec c) = vec a * vec b + vec a * vec c$$
- 乘以标量时满足 $$ (c_1 vec a) * (c_2 vec b) = (c_1 c_2)(vec a * vec b)$$
- 不满足结合律。因为标量 $$ vec a * vec b $$ 与向量 $$ vec c $$ 的点积没有定义,所以$$(vec a * vec b) * vec c=vec a * (vec b * vec c)$$ 没有意义。
点积的代数定义简单实用,易于表示,也易于使用计算机程序处理。是线性代数的基本操作之一。
5. 点积的几何意义
对于任何一个n维向量有 $|vec a|^2=a_1^2+a_2^2+…+a_n^2$。根据勾股定理,这是很显然的。换个角度说如果没有勾股定理,这一步就不存在,后面的内容也不存在了。而勾股定理不是由代数方法证明的,而是独立于代数系统之外的空间基本性质。而空间和时间是宇宙最根本的本质。这就是勾股定理最神奇的地方。
我们根据点积的定义可知:$$ vec a * vec a = a_1 * a_1 + a_2 * a_2 + … a_n * a_n = |vec a|^2$$ 即 $$ vec a * vec a == |vec a|^2$$
我们根据余弦定理的向量表示可得:$$ vec c * vec c = vec a * vec a + vec b * vec b - 2 |vec a| |vec b| cos theta . (1)$$
根据向量的定义 $$ vec c = vec a - vec b $$ 有 $$ vec c * vec c = (vec a - vec b) * (vec a - vec b) = vec a * vec a + vec b * vec b - 2 vec a * vec b . (2)$$
结合等式$$(1)$$、$$(2)$$有 $$vec a * vec b = |vec a| |vec b| cos theta$$。一个看似简单的代数点积操作,竟然和夹角余弦相关,真是不可思议。
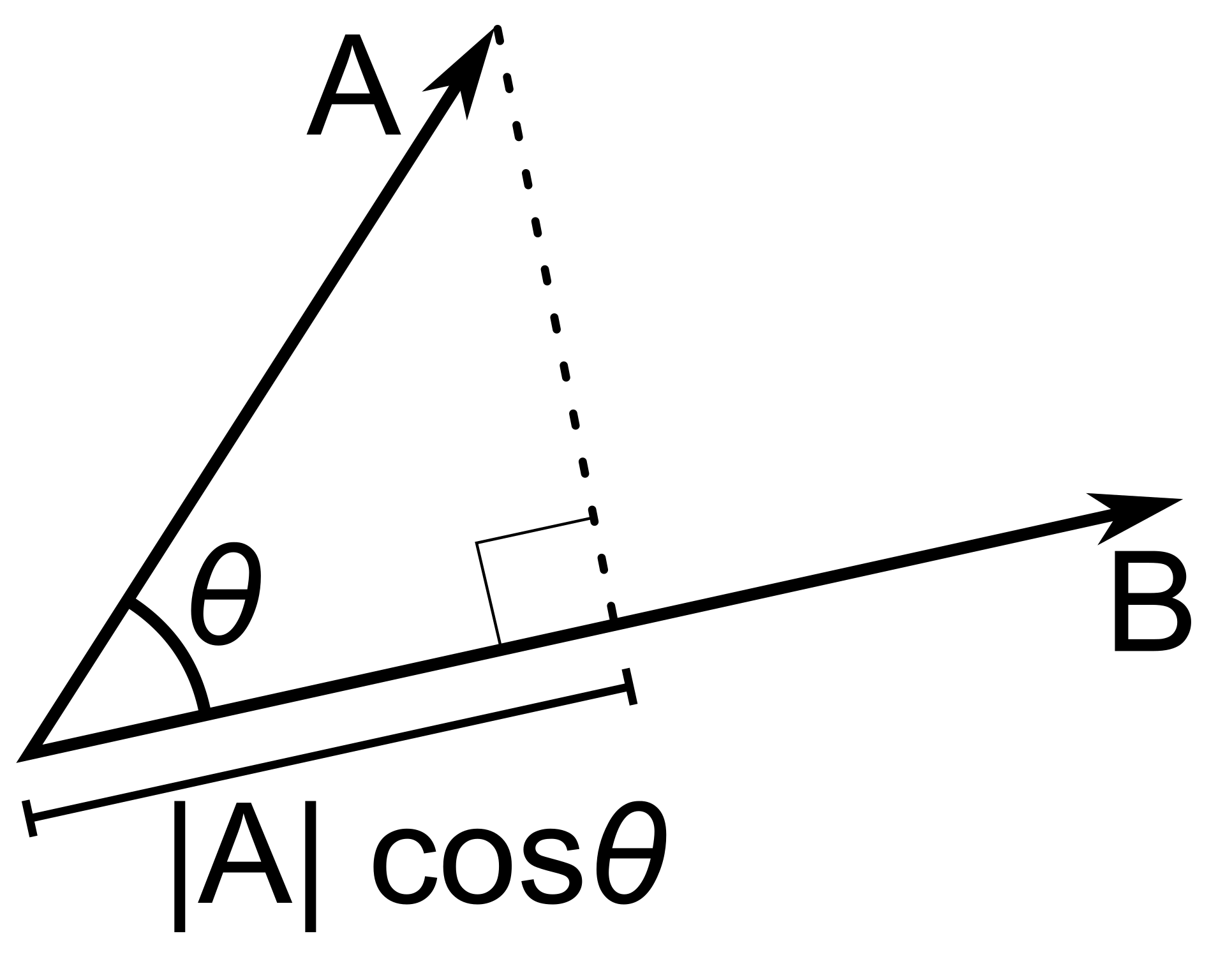
点积的几何意义是什么呢?关键就在这个$cos theta$,如果$$|vec b|$$为1时候,我们可以将$$vec a * vec b$$视为$$vec a $$在$$vec b$$方向上的投影长度。
6. 点积的物理意义(从数学到宇宙)
点积的物理意义就是向量在某方向上的投影长度。这在物理上可以表达力在某方向上的投影,光在某方向的投影,速度、加速度在某方向的投影。而点积的操作,可以使我们只需要关心这些物理量的向量表示,而不需要去关心夹角,不需要去计算三角函数。而在统计学、机器学习等方面,余弦可以表示两个向量之间的相似性,比如两个词向量,两个用户的兴趣向量等,应用非常广泛。下面就以计算机图形学举例来说明点积的应用。
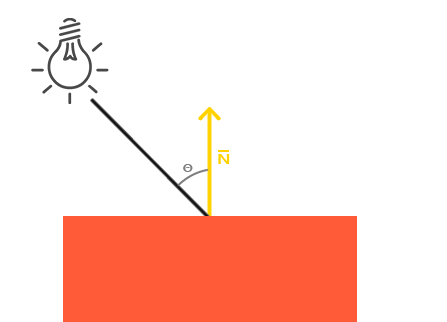
冯氏光照模型将一个物体的光照分解为环境光+漫反射光+镜面反射光。

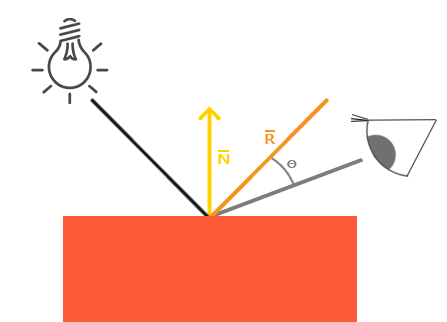
环境光比较简单就是一个常量。而漫反射光,则为光照强度在平面的法线方向的投影,与法线方向一致则光照最强。镜面反射光则为反射光方向在视角方向上的投影,与视角完全一致,则反射光最强。
OpenGL的shader大致如下:
1 |
|