DQN证明了深度学习在增强学习中的可行性。深度学习可以将复杂的概念隐含在网络之中。但是DQN并没有将所有的概念都隐含在网络之中,只是把Q值的计算放在了网络之中,比如`epsilon-greedy`动作选择策略。因为如何选择动作和如何通过Q值计算出目标值,都是DQN所面临的问题,而Q值的目的也是为了选择动作。我们可以将增加学习的问题简化为选择动作的问题。那么我们可否使用深度学习直接做出动作选择呢?显然,我们可以定义一个网络`pi_theta`,其中输入为状态`s`,输出为每个动作`a`的概率。
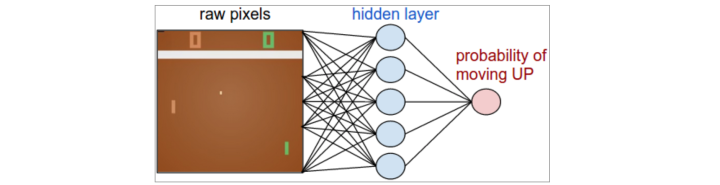
因为这个网络与策略函数的定义一样,所以被称为策略网络。`pi_theta(a|s)`,表示在`s`状态下选择动作`a`的概率。只要这个网络能够收敛,我们就可以直接得到最佳策略。这个网络的奖励函数也就是最终游戏的总奖励。
`J(theta) = sum_(s in S)d^pi(s)V^pi(s) = sum_(s in S)d^pi(s)sum_(a in A)pi_theta(a|s)Q^pi(s, a)`
`d^pi(s)`指状态`s`在马尔科夫链上的稳定分布,`d^pi(s) = lim_(t->oo)P(s_t=s|s_0,pi_theta)`。
但是这个表达式看上去是不可能计算的,因为状态的分布和Q值都是随着策略的更新而不断变化的。但是我们并不需要计算`J(theta)`,在梯度下降法中我们只需要计算梯度`grad_(theta)J(theta)`即可
`grad_(theta)V^pi(s)`
`= grad_(theta)(sum_(a in A)pi_theta(a|s)Q^pi(s, a))`
根据导数乘法规则
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)grad_thetaQ^pi(s, a))`
展开`Q^pi(s,a)`为各各种可能的下一状态奖励之和
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)grad_(theta)sum_(s’,r)P(s’,r|s,a)(r+V^pi(s’)))`
而其中状态转移函数`P(s’,r|s,a)`、奖励`r`由环境决定,与`grad_theta`无关,所以
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)sum_(s’,r)P(s’,r|s,a)grad_(theta)V^pi(s’))`
`= sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)sum_(s’)P(s’|s,a)grad_(theta)V^pi(s’))`
现在我们有了一个形式非常好的递归表达式:
`grad_(theta)V^pi(s) = sum_(a in A)(grad_(theta)pi_(theta)Q^pi(s, a)+pi_(theta)(a|s)sum_(s’)P(s’|s,a)grad_(theta)V^pi(s’))`
设 `rho^pi(s->x, k)` 表示在策略`pi^theta`下,`k`步以后状态`s`转移到状态`x`的概率。有:
- `rho^pi(s->s, k=0)=1`
- `rho^pi(s->s’, k=1)=sum_(a)pi_(theta)(a|s)P(s’|s,a)`
- `rho^pi(s->x, k+1) = sum_(s’)rho^pi(s->s’, k)rho^pi(s’->x, 1)`
为了简化计算,令 `phi(s)=sum_(a in A)grad_(theta)pi_theta(a|s)Q^pi(s,a)`
`grad_(theta)V^pi(s)`
`= phi(s) + sum_(a in A)pi_(theta)(a|s)sum_(s’)P(s’|s,a)grad_(theta)V^pi(s’) `
`= phi(s) + sum_(s’)sum_(a in A)pi_(theta)(a|s)P(s’|s,a)grad_(theta)V^pi(s’) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)grad_(theta)V^pi(s’) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)(phi(s’) + sum_(s’’)rho^pi(s’->s’’,1)grad_(theta)V^pi(s’’)) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)phi(s’) + sum_(s’’)rho^pi(s->s’’,2)grad_(theta)V^pi(s’’) `
`= phi(s) + sum_(s’)rho^pi(s->s’,1)phi(s’) + sum_(s’’)rho^pi(s->s’’,2)phi(s’’) + sum_(s’’’)rho^pi(s->s’’’,3)grad_(theta)V^pi(s’’’) `
`= …`
`= sum_(x in S)sum_(k=0)^(oo)rho^pi(s->x, k)phi(x)`
令 `eta(s)=sum_(k=0)^(oo)rho^pi(s_0->s, k)`
`grad_(theta)J(theta)=grad_(theta)V^pi(s_0)`
`= sum_(s)sum_(k=0)^(oo)rho^pi(s_0->s,k)phi(s)`
`= sum_(s)eta(s)phi(s)`
`= (sum_(s)eta(s))sum_(s)((eta(s))/(sum_(s)eta(s)))phi(s)`
因 `sum_(s)eta(s)` 属于常数,对于求梯度而言常数可以忽略。
`prop sum_(s)((eta(s))/(sum_(s)eta(s)))phi(s)`
因 `eta(s)/(sum_(s)eta(s))`表示`s`的稳定分布
`= sum_(s)d^pi(s)sum_a grad_(theta)pi_(theta)(a|s)Q^pi(s,a)`
`= sum_(s)d^pi(s)sum_a pi_(theta)(a|s)Q^pi(s,a)(grad_(theta)pi_(theta)(a|s))/(pi_(theta)(a|s))`
因 ` (ln x)’ = 1/x `
`= Err_pi[Q^pi(s,a)grad_theta ln pi_theta(a|s)]`
所以得出策略梯度最重要的定理:
` grad_(theta)J(theta)=Err_pi[Q^pi(s,a)grad_theta ln pi_theta(a|s)] `
其中的`Q^pi(s,a)`也就是状态s的累计收益,可以在一次完整的动作轨迹中累计计算得出。
算法描述
该算法被称为 REINFORCE
- 随机初始化`theta`
- 生成一个完整的策略`pi_theta`的轨迹: `S1,A1,R2,S2,A2,…,ST`。
- For t=1, 2, … , T-1:
- ` v_t = sum_(i=0)^(oo) gamma^i R_(t+i+1) `
- ` theta larr theta + alpha v_t ln pi_theta (A_t|S_t) `